题目内容
17.方程组$\left\{\begin{array}{l}{(x+1)^{2}+(y-5)^{2}=27}\\{x+y=1}\end{array}\right.$的解为$\left\{\begin{array}{l}{{x}_{1}=\frac{-5+3\sqrt{5}}{2}}\\{{y}_{1}=\frac{7-3\sqrt{5}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{-5-3\sqrt{5}}{2}}\\{{y}_{2}=\frac{7+3\sqrt{5}}{2}}\end{array}\right.$.分析 把x+y=1化为y=1-x后代入第一个方程,解关于x的一元二次方程即可.
解答 解:$\left\{\begin{array}{l}{(x+1)^{2}+(y-5)^{2}=27①}\\{x+y=1②}\end{array}\right.$,
由②得,y=1-x③,
把③代入①得,x2+5x-5=0
解得,x1=$\frac{-5+3\sqrt{5}}{2}$,x2=$\frac{-5-3\sqrt{5}}{2}$,
把x1=$\frac{-5+3\sqrt{5}}{2}$,x2=$\frac{-5-3\sqrt{5}}{2}$代入③得,
y1=$\frac{7-3\sqrt{5}}{2}$,y2=$\frac{7+3\sqrt{5}}{2}$,
故答案为:$\left\{\begin{array}{l}{{x}_{1}=\frac{-5+3\sqrt{5}}{2}}\\{{y}_{1}=\frac{7-3\sqrt{5}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{-5-3\sqrt{5}}{2}}\\{{y}_{2}=\frac{7+3\sqrt{5}}{2}}\end{array}\right.$.
点评 本题考查的是二元二次方程组的解法,掌握代入法解方程组是解题的关键.运用代入法先消去一个未知数,再解关于另一个未知数的一元二次方程,把求得结果代入一个较简单的方程中即可.

练习册系列答案
相关题目
7.已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )
| A. | 3 | B. | 5 | C. | 8 | D. | 11 |
8.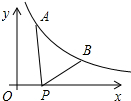 如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
 如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )| A. | (0.5,0) | B. | (1,0) | C. | (1.5,0) | D. | (2.5,0) |
2.计算2-3的结果是( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
 已知,正六边形ABCDEF在直角坐标系内的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2015次翻转之后,点B的坐标是(4031,$\sqrt{3}$).
已知,正六边形ABCDEF在直角坐标系内的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2015次翻转之后,点B的坐标是(4031,$\sqrt{3}$).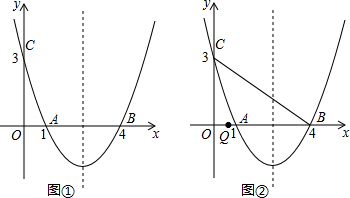
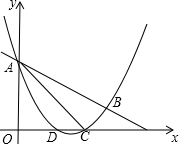 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),C(3,0).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),C(3,0).