题目内容
3. 如图,∠1=∠2,BC=CE,请补充一个条件:AC=DC(写一种即可),使得△ABC≌△DEC.
如图,∠1=∠2,BC=CE,请补充一个条件:AC=DC(写一种即可),使得△ABC≌△DEC.
分析 已知∠1=∠2,就是已知∠ACB=∠DCE,则根据三角形的判定定理即可证得.
解答 解:可以添加AC=DC,
理由是:∵∠1=∠2,
∴∠ACB=∠DCE,
∴在△ABC和△DEC中,
$\left\{\begin{array}{l}{AC=DC}\\{∠ACB=∠DCE}\\{BC=CE}\end{array}\right.$,
∴△ABC≌△DEC.
故答案是:AC=DC.(答案不唯一).
点评 本题考查了三角形全等的判定,正确理解判定定理是关键.

练习册系列答案
相关题目
11.下列命题是真命题的是( )
| A. | 若a>b,则ac>bc | B. | 若ac>bc,则a>b | C. | 若a>b,则ac2>bc2 | D. | 若ac2>bc2,则a>b |
18. 一副三角板如图叠放在一起,∠α的度数为( )
一副三角板如图叠放在一起,∠α的度数为( )
 一副三角板如图叠放在一起,∠α的度数为( )
一副三角板如图叠放在一起,∠α的度数为( )| A. | 95° | B. | 100° | C. | 105° | D. | 120° |
12.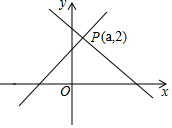 如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
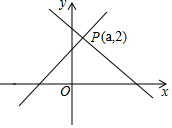 如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )| A. | x≥-1 | B. | 0≤x≤1 | C. | x≥1 | D. | x≤1 |
