题目内容
3. 如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.
如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.
分析 如图,作AE⊥l3于E,CF⊥l3于F.首先证明△ABE≌△BCF,推出AE=BF=3,BE=CF=5,求出AB2、BC2即可解决问题.
解答 解:如图,作AE⊥l3于E,CF⊥l3于F.
∵∠ABC=∠AEB=∠CFB=90°,
∴∠ABE+∠CBF=90°,∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{∠ABE=∠BCF}\\{∠AEB=∠CFB}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCF,
∴AE=BF=3,BE=CF=5,
∴BC2=AB2=32+52=34,
∴AC2=BC2+AB2=68.
点评 本题考查全等三角形判定和性质、勾股定理、等腰直角三角形的性质、平行线的性质等知识,解题的关键是学会添加常用辅助线面构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.和半径相等的弦所对的圆周角的度数是( )
| A. | 60° | B. | 30° | C. | 150° | D. | 30°和150° |
18.已知一次函数y=3x+2的图象绕坐标原点旋转180度后的一次函数的表达式为( )
| A. | y=-3x+2 | B. | y=3x-2 | C. | y=-3x-2 | D. | y=2x-3 |
8.在平面直角坐标系xOy中,函数y=x2的图象经过点M(x1,y1),N(x2,y2)两点,若-4<x1<-2,0<x2<2,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1≤y2 | C. | y1>y2 | D. | y1≥y2 |
15.下列各式中,正确的是( )
| A. | (a2)3=a5 | B. | a+a=a2 | C. | a4÷a3=a1 | D. | -3a+3b=-3(a-b) |
12. 河堤横断面如图所示,坝高BC=6米,迎水坡AB的坡长比为1:$\sqrt{3}$,则AB的长为( )
河堤横断面如图所示,坝高BC=6米,迎水坡AB的坡长比为1:$\sqrt{3}$,则AB的长为( )
 河堤横断面如图所示,坝高BC=6米,迎水坡AB的坡长比为1:$\sqrt{3}$,则AB的长为( )
河堤横断面如图所示,坝高BC=6米,迎水坡AB的坡长比为1:$\sqrt{3}$,则AB的长为( )| A. | 5$\sqrt{3}$米 | B. | 4$\sqrt{3}$米 | C. | 12米 | D. | 6$\sqrt{3}$米 |
13.下列运算正确的是( )
| A. | $\sqrt{4}$+$\sqrt{9}$=$\sqrt{13}$ | B. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | C. | $\frac{\sqrt{a}}{\sqrt{9b}}$=$\frac{\sqrt{a}}{3b}$ | D. | $\sqrt{\frac{3a}{2{b}^{4}}}$=$\frac{\sqrt{6a}}{2{b}^{2}}$ |
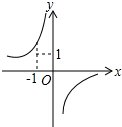 已知反比例函数y=$\frac{k}{x}$的图象如图,则二次函数y=2kx2-2x+k2的图象大致为( )
已知反比例函数y=$\frac{k}{x}$的图象如图,则二次函数y=2kx2-2x+k2的图象大致为( )