题目内容
14.甲、乙两家商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案,在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超过50元的部分按95%收费.某顾客购买x元的该商品.(1)当0<x≤50时,请直接回答该顾客在甲、乙两家商场购物花费的关系;
(2)当50<x≤100时,到哪家商场购物花费少?少花多少钱?(用含x的代数式表示)
(3)当x>100时,到哪家商场购物花费少?
分析 设累计购物x元,分别表示出在甲乙两商场的花费,列不等式,分情况讨论,求出最合适的消费方案.
解答 解:(1)当累计购物不超过50元时,在甲乙两商场的花费一样;
②当累计消费超过50元而不超过100元时,在乙商场享受优惠,在甲商场不享受优惠,因此应该到乙商场购买;
③当累计消费超过100元时,设累计消费x元(x>100),
甲商场消费为:100+(x-100)×0.9元,
在乙商场消费为:50+(x-50)×0.95元,
当100+(x-100)×0.9>50+(x-50)×0.95,解得:x<150,
当100+(x-100)×0.9<50+(x-50)×0.95,解得:x>150,
当100+(x-100)×0.9=50+(x-50)×0.95,解得:x=150,
综上所述,当累计消费大于100元少于150元时,在乙商店花费少;
当累计消费大于150元时,在甲商店花费少;
当累计消费等于150元或不超过50元时,在甲乙商场花费一样.
点评 本题考查了一元一次不等式的应用,解答本题的关键是读懂题意,将现实生活中的事件与数学思想联系起来,列出不等式关系式即可求解.注意此题分类讨论的数学思想.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
5.抛物线y=(x-5)2+6的对称轴是( )
| A. | 直线x=-5 | B. | 直线x=5 | C. | 直线x=-6 | D. | 直线x=6 |
2.估计$\sqrt{6}$的值在( )
| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
9.根据分式的基本性质,分式$\frac{-a}{a-2b}$可变形为( )
| A. | $\frac{a}{a+2b}$ | B. | $\frac{a}{-a-2b}$ | C. | $-\frac{a}{a+2b}$ | D. | $-\frac{a}{a-2b}$ |
19.如图①是一个正三棱柱毛坯,将其截去一部分,得到一个工件如图②,这个工件的俯视图是( )


| A. | a | B. | c | C. | d | D. | b |
4.如果|x-2|+(y+3)2=0,那么x+y等于( )
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |

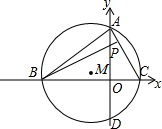 如图,在平面直角坐标系中,A(0,6),P(0,4),点C为x轴正半轴上任一点,BP⊥AC交x轴于B点,△ABC内接于⊙M交y轴负半轴于D点.
如图,在平面直角坐标系中,A(0,6),P(0,4),点C为x轴正半轴上任一点,BP⊥AC交x轴于B点,△ABC内接于⊙M交y轴负半轴于D点. 如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.
如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.