题目内容
11.和半径相等的弦所对的圆周角的度数是( )| A. | 60° | B. | 30° | C. | 150° | D. | 30°和150° |
分析 根据题意画出相应的图形,如图所示,由半径等于弦长,得到三角形AOB为等边三角形,利用等边三角形的性质得到∠AOB为60°,利用同弧所对的圆心角等于所对圆周角的2倍求出∠ACB的度数,再利用圆内接四边形的对角1互补求出∠ADB的度数,即可得出弦AB所对圆周角的度数.
解答 解:根据题意画出相应的图形,如图所示,
∵OA=OB=AB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∵∠AOB与∠ACB都对$\widehat{AB}$,
∴∠ACB=$\frac{1}{2}$∠AOB=30°,
又四边形ACBD为圆O的内接四边形,
∴∠ACB+∠ADB=180°,
∴∠ADB=150°,
则弦AB所对的圆周角为30°或150°.
故答案为:30°或150
点评 此题考查了圆周角定理,等边三角形的性质,以及圆内接四边形的性质,熟练掌握圆周角定理是解本题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
2.估计$\sqrt{6}$的值在( )
| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
19.如图①是一个正三棱柱毛坯,将其截去一部分,得到一个工件如图②,这个工件的俯视图是( )


| A. | a | B. | c | C. | d | D. | b |
20. 已知:如图,在△ABC中,∠A=45°,sinB=$\frac{1}{3}$,AC=$\sqrt{2}$,那么AB的长度是( )
已知:如图,在△ABC中,∠A=45°,sinB=$\frac{1}{3}$,AC=$\sqrt{2}$,那么AB的长度是( )
 已知:如图,在△ABC中,∠A=45°,sinB=$\frac{1}{3}$,AC=$\sqrt{2}$,那么AB的长度是( )
已知:如图,在△ABC中,∠A=45°,sinB=$\frac{1}{3}$,AC=$\sqrt{2}$,那么AB的长度是( )| A. | 1+2$\sqrt{2}$ | B. | 1+$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 9 |
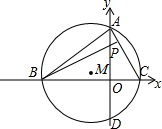 如图,在平面直角坐标系中,A(0,6),P(0,4),点C为x轴正半轴上任一点,BP⊥AC交x轴于B点,△ABC内接于⊙M交y轴负半轴于D点.
如图,在平面直角坐标系中,A(0,6),P(0,4),点C为x轴正半轴上任一点,BP⊥AC交x轴于B点,△ABC内接于⊙M交y轴负半轴于D点. 四边形ABCD中,E、F分别是BD、AC中点,求证:三角形EFG面积等于四边形AEFD的面积.
四边形ABCD中,E、F分别是BD、AC中点,求证:三角形EFG面积等于四边形AEFD的面积. 如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.
如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.