题目内容
18.已知一次函数y=3x+2的图象绕坐标原点旋转180度后的一次函数的表达式为( )| A. | y=-3x+2 | B. | y=3x-2 | C. | y=-3x-2 | D. | y=2x-3 |
分析 根据关于原点对称的点的坐标特征即可求解.
解答 解:一次函数y=3x+2的图象绕坐标原点旋转180度后的一次函数的表达式为:-y=-3x+2,即y=3x-2.
故选B.
点评 本题考查了一次函数图象与几何变换,对于直线y=kx+b(k≠0,且k,b为常数),
①关于x轴对称,就是x不变,y变成-y:-y=kx+b,即y=-kx-b(关于X轴对称,横坐标不变,纵坐标是原来的相反数);
②关于y轴对称,就是y不变,x变成-x:y=k(-x)+b,即y=-kx+b(关于y轴对称,纵坐标不变,横坐标是原来的相反数);
③关于原点对称,就是x和y都变成相反数:-y=k(-x)+b,即y=kx-b(关于原点轴对称,横、纵坐标都变为原来的相反数).

练习册系列答案
相关题目
8. 如图,AB和CD是⊙O的两条直径,弦DE∥AB,∠DOE=50°,那么∠BOD为( )
如图,AB和CD是⊙O的两条直径,弦DE∥AB,∠DOE=50°,那么∠BOD为( )
 如图,AB和CD是⊙O的两条直径,弦DE∥AB,∠DOE=50°,那么∠BOD为( )
如图,AB和CD是⊙O的两条直径,弦DE∥AB,∠DOE=50°,那么∠BOD为( )| A. | 115° | B. | 100° | C. | 80° | D. | 65° |
9.根据分式的基本性质,分式$\frac{-a}{a-2b}$可变形为( )
| A. | $\frac{a}{a+2b}$ | B. | $\frac{a}{-a-2b}$ | C. | $-\frac{a}{a+2b}$ | D. | $-\frac{a}{a-2b}$ |
7. 如图,直线AB∥CD,AF交CD于点E,AG平分∠FAB,∠CEF=140°,则∠GAB等于( )
如图,直线AB∥CD,AF交CD于点E,AG平分∠FAB,∠CEF=140°,则∠GAB等于( )
 如图,直线AB∥CD,AF交CD于点E,AG平分∠FAB,∠CEF=140°,则∠GAB等于( )
如图,直线AB∥CD,AF交CD于点E,AG平分∠FAB,∠CEF=140°,则∠GAB等于( )| A. | 35° | B. | 20° | C. | 45° | D. | 50° |
8. 如图直线l1∥l2∥l3,直线l4、l5分别交l1、l2、l3于A、B、C、E、F、D,且EF=4、DE=3、AB=1.2、则AC的长为( )
如图直线l1∥l2∥l3,直线l4、l5分别交l1、l2、l3于A、B、C、E、F、D,且EF=4、DE=3、AB=1.2、则AC的长为( )
 如图直线l1∥l2∥l3,直线l4、l5分别交l1、l2、l3于A、B、C、E、F、D,且EF=4、DE=3、AB=1.2、则AC的长为( )
如图直线l1∥l2∥l3,直线l4、l5分别交l1、l2、l3于A、B、C、E、F、D,且EF=4、DE=3、AB=1.2、则AC的长为( )| A. | 0.9 | B. | 1.6 | C. | 2.8 | D. | 2.1 |
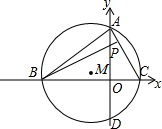 如图,在平面直角坐标系中,A(0,6),P(0,4),点C为x轴正半轴上任一点,BP⊥AC交x轴于B点,△ABC内接于⊙M交y轴负半轴于D点.
如图,在平面直角坐标系中,A(0,6),P(0,4),点C为x轴正半轴上任一点,BP⊥AC交x轴于B点,△ABC内接于⊙M交y轴负半轴于D点.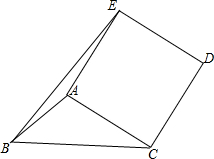 如图,在△ABC中,∠ABC=45°,AB=$\sqrt{2}$,BC=4,以AC为边在AC的右侧作正方形ACDE,连接BE,求BE的长.
如图,在△ABC中,∠ABC=45°,AB=$\sqrt{2}$,BC=4,以AC为边在AC的右侧作正方形ACDE,连接BE,求BE的长. 如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.
如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.