题目内容
 甲乙两船同时从港口O出发,甲船以16.1海里/小时的速度向东偏南35°方向航行,乙船向西偏南58°方向航行,航行了两小时,甲船到达A处并观测到B处的乙船恰好在其正西方向.求乙船的速度v(精确到0.1海里/小时).
甲乙两船同时从港口O出发,甲船以16.1海里/小时的速度向东偏南35°方向航行,乙船向西偏南58°方向航行,航行了两小时,甲船到达A处并观测到B处的乙船恰好在其正西方向.求乙船的速度v(精确到0.1海里/小时).考点:解直角三角形的应用-方向角问题
专题:
分析:本题可以求出船行进的距离OA,根据三角函数就可以求出OB,就可以求出乙船的速度.
解答: 解:(1)由题可知:OA=16.1×2=32.2(海里).
解:(1)由题可知:OA=16.1×2=32.2(海里).
(2)∠A=35°,∠B=58°,
则在Rt△OCA中,sinA=
=sin35°.
∴OC=OA•sin35°≈21.78(海里).
在Rt△OBC中,sinB=
=sin58°,
∴OB=
≈21.78(海里).
∴V乙=
≈10.89(海里/时).
答:求甲船从港口O到A处的航行距离是32.2海里;求乙船的速度V约是10.89海里/时.
 解:(1)由题可知:OA=16.1×2=32.2(海里).
解:(1)由题可知:OA=16.1×2=32.2(海里).(2)∠A=35°,∠B=58°,
则在Rt△OCA中,sinA=
| OC |
| OA |
∴OC=OA•sin35°≈21.78(海里).
在Rt△OBC中,sinB=
| OC |
| OB |
∴OB=
| OC |
| sin58° |
∴V乙=
| 21.78 |
| 2 |
答:求甲船从港口O到A处的航行距离是32.2海里;求乙船的速度V约是10.89海里/时.
点评:本题主要考查三角函数的定义,理解方向角的定义是解决本题的关键.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AB的中点,且DC=AD+BC,则下列结论中错误的有( )
如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AB的中点,且DC=AD+BC,则下列结论中错误的有( )| A、DE平分∠ADC |
| B、△DEC是直角三角形 |
| C、点E到DC的距离为AB长的一半 |
| D、△DEC的面积为△ADE面积的2倍 |
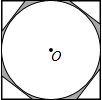 已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )A、32
| ||
B、
| ||
| C、1 | ||
| D、16-4π |

 如图,GC交AB于点M,GH分别交AB,EF于点N,HD平分∠GHF,∠1+∠C=180°,∠2=∠3=60°,求证:CD∥EF.
如图,GC交AB于点M,GH分别交AB,EF于点N,HD平分∠GHF,∠1+∠C=180°,∠2=∠3=60°,求证:CD∥EF. 上海世博会中国馆共分为国家馆和地区馆两部分,国家馆居中升起、层叠出挑,采用极富中国建筑文化元素的红色“斗冠”造型,由地下一层、地上六层组成.小明通过上网查阅资料得知,国家馆地上六层均为正方形,如图所示,最上面一层正方形边长为a米,以下每层的边长比上一层减少b米.
上海世博会中国馆共分为国家馆和地区馆两部分,国家馆居中升起、层叠出挑,采用极富中国建筑文化元素的红色“斗冠”造型,由地下一层、地上六层组成.小明通过上网查阅资料得知,国家馆地上六层均为正方形,如图所示,最上面一层正方形边长为a米,以下每层的边长比上一层减少b米. 如图,以O为圆心,任意长为半径画弧,与射线OM相交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( )
如图,以O为圆心,任意长为半径画弧,与射线OM相交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( )