题目内容
6．若$\frac{b}{a}$=$\frac{5}{3}$，则$\frac{a+b}{a-b}$的值是（ ）| A． | $\frac{1}{4}$ | B． | -$\frac{1}{4}$ | C． | 4 | D． | -4 |
分析 根据等式的性质，可用a表示b，根据分式的性质，可得答案．
解答 解：由$\frac{b}{a}$=$\frac{5}{3}$，得
b=$\frac{5a}{3}$．
$\frac{a+b}{a-b}$=$\frac{a+\frac{5a}{3}}{a-\frac{5a}{3}}$=$\frac{\frac{8a}{3}}{-\frac{2a}{3}}$=-4，
故选：D．
点评 本题考查了比例的性质，利用等式的性质得出b=$\frac{5a}{3}$是解题关键，又利用了分式的性质．
练习册系列答案
相关题目
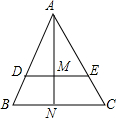如图，已知△ABC中，DE∥BC，DE=8，BC=12，AN⊥BC交DE于M，四边形BCED的面积为90．求△ADE的面积及AM、AN的长．
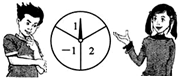如图，一转盘被等分成三个扇形，上面分别标有-1，2，指针位置固定，转动转盘后任其自由停止后，某个扇形会恰好停在指针所指的位置，得到这个扇形上相应的数．若指针恰好指在等分线上，则需重新转动转盘．
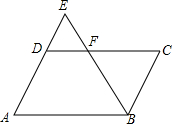如图，点F是?ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论正确的有（ ）