题目内容
16.关于x、y的多项式mx3+3nxy2+2x3-xy2+2x2+4不含三次项,求2m+3n的值.分析 根据合并同类项,可化简整式,根据多项式不含三次项,可得三次项的系数为零,可得m、n的值,根据代数式求值,可得答案.
解答 解;原式=(m+2)x3+(3n-1)xy2+2x2+4,
由多项式mx3+3nxy2+2x3-xy2+2x2+4不含三次项,得
m+2=0,3n-1=0.
解得m=-2$\frac{1}{3}$,n=$\frac{1}{3}$.
当m=-2,n=$\frac{1}{3}$时,2m+3n=2×(-2)+3×$\frac{1}{3}$=-4+1=-3.
故2m+3n的值为-3.
点评 本题考查了多项式,先化简整式,在确定项的系数,最后代数式求值.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
6.若$\frac{b}{a}$=$\frac{5}{3}$,则$\frac{a+b}{a-b}$的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -4 |
7.若△ABC中,AB=25cm,AC=26cm,高AD=24cm,则BC的长为( )cm.
| A. | 17或3 | B. | 3 | C. | 17 | D. | 以上都不对 |
4.我国全国第五次人口普查结果显示,我国总人口已达到13亿,用科学记数法表示这个数,结果正确的是( )
| A. | 0.13×1010 | B. | 1.3×109 | C. | 13×108 | D. | 130×107 |
5.如果3x=2y(x、y均不为零),那么x:y的值是( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
6.抛物线y=ax2+4ax-5的对称轴为( )
| A. | x=-2a | B. | x=4 | C. | x=2a | D. | x=-2 |
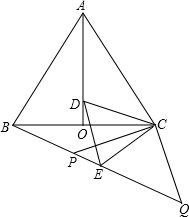 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.