题目内容
1.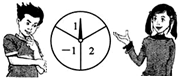 如图,一转盘被等分成三个扇形,上面分别标有-1,2,指针位置固定,转动转盘后任其自由停止后,某个扇形会恰好停在指针所指的位置,得到这个扇形上相应的数.若指针恰好指在等分线上,则需重新转动转盘.
如图,一转盘被等分成三个扇形,上面分别标有-1,2,指针位置固定,转动转盘后任其自由停止后,某个扇形会恰好停在指针所指的位置,得到这个扇形上相应的数.若指针恰好指在等分线上,则需重新转动转盘.(1)若小静转动转盘一次,则她得到负数的概率为$\frac{1}{3}$;
(2)小宇和小静分别转动转盘一次,若两人得到的数相同,则称两人“不谋而合”.请用列表法(或画树状图)求出两人“不谋而合”的概率.
分析 (1)直接利用概率公式求出得到负数的概率;
(2)转动2次的数字均为1,-1,2,可用树状图列举出所有情况,进而求出概率.
解答 解:(1)小静转动转盘一次,则她得到负数的概率为:$\frac{1}{3}$.
故答案为:$\frac{1}{3}$;
(2)画树状图:
∵所有的可能有9种,两人得到的数相同的有3种,
∴P(不谋而合)=$\frac{3}{9}=\frac{1}{3}$.
点评 此题主要考查了树状图法求概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若$\frac{b}{a}$=$\frac{5}{3}$,则$\frac{a+b}{a-b}$的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -4 |
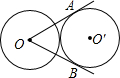 两个等圆⊙O和⊙O′外切,过⊙O作⊙O′的两条切线OA、OB、A、B是切点,则∠AOB等于多少度?
两个等圆⊙O和⊙O′外切,过⊙O作⊙O′的两条切线OA、OB、A、B是切点,则∠AOB等于多少度?