题目内容
16.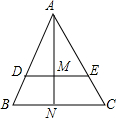 如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.
如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.
分析 根据DE∥BC,得到△ADE∽△ABC,根据相似三角形的性质得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=($\frac{8}{12}$)2=$\frac{4}{9}$,即可得到△ADE的面积=72,根据平行线的性质得到AM⊥DE,根据三角形的面积公式列方程即可得到结论.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=($\frac{8}{12}$)2=$\frac{4}{9}$,
∵四边形BCED的面积为90,
∴$\frac{{S}_{△ADE}}{{S}_{△ADE}+90}$=$\frac{4}{9}$,
∴△ADE的面积=72,
∵DE∥BC,AN⊥BC,
∴AM⊥DE,
∴$\frac{1}{2}$DE•AM=72,$\frac{1}{2}$BC•AN=162,
∴AM=12,AN=17.
点评 本题考查了相似三角形的判定和性质,图形面积的计算,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
8.已知等腰△ABC的两边长分别为2和4,则等腰△ABC的周长为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 12 |
5.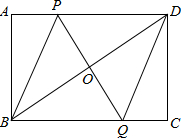 如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=4厘米,AB=3厘米,当AP为何值时,四边形PBQD是菱形,并加以说明.
 如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.(1)求证:OP=OQ;
(2)若AD=4厘米,AB=3厘米,当AP为何值时,四边形PBQD是菱形,并加以说明.
6.若$\frac{b}{a}$=$\frac{5}{3}$,则$\frac{a+b}{a-b}$的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -4 |
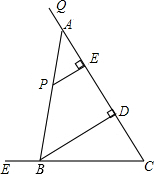 如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.
如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.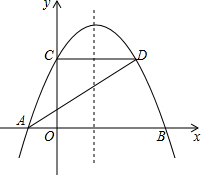 如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).
如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).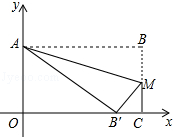 矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知
矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知