题目内容
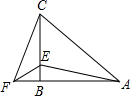 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=35°,求∠ACF度数.
考点:全等三角形的判定与性质
专题:
分析:(1)根据HL可直接证明Rt△ABE≌Rt△CBF;
(2)先求得∠BAE的度数,再由(1)得出∠BCF的度数,从而得出∠ACF度数.
(2)先求得∠BAE的度数,再由(1)得出∠BCF的度数,从而得出∠ACF度数.
解答:解:(1)∵∠ABC=90°,
∴∠CBF=∠ABE=90°
在Rt△ABE和Rt△CBF中,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°,
∵∠BAE=∠CAB-∠CAE=45°-35°=10°.
由(1)知 Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=10°,
∴∠ACF=∠BCF+∠ACB=45°+10°=55°.
∴∠CBF=∠ABE=90°
在Rt△ABE和Rt△CBF中,
|
∴Rt△ABE≌Rt△CBF(HL);
(2)∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°,
∵∠BAE=∠CAB-∠CAE=45°-35°=10°.
由(1)知 Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=10°,
∴∠ACF=∠BCF+∠ACB=45°+10°=55°.
点评:本题考查了全等三角形的判定和性质,明确全等三角形的判定方法是解决本题关键,属于中等题目.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
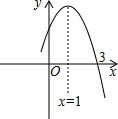 若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为( )
若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为( )| A、-2 | B、-1 | C、0 | D、1 |
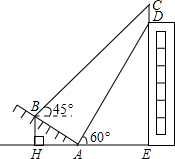 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1: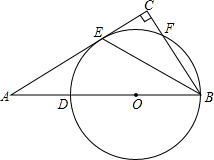 如图,Rt△ABC中,∠C=90°,D在AB上,BE平分∠ABC交AC于点E,以BD为直径的圆经过点E,交BC于点F.
如图,Rt△ABC中,∠C=90°,D在AB上,BE平分∠ABC交AC于点E,以BD为直径的圆经过点E,交BC于点F.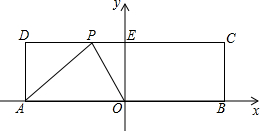 如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标.
如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标. 如图,AB⊥BD,ED⊥BD,C是BD上的一点,BC=DE,AB=CD.求证:AC⊥CE.
如图,AB⊥BD,ED⊥BD,C是BD上的一点,BC=DE,AB=CD.求证:AC⊥CE.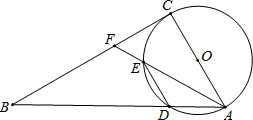 如图,以Rt△ABC的边AC为直径的⊙O交斜边AB于点D,点F为BC上一点,AF交⊙O于点E,且DE∥AC.
如图,以Rt△ABC的边AC为直径的⊙O交斜边AB于点D,点F为BC上一点,AF交⊙O于点E,且DE∥AC.