题目内容
已知二次函数y=x2-2x+k-1,当x取一切实数时,函数值y恒为正值,则k的取值范围是 .
考点:抛物线与x轴的交点
专题:
分析:由二次函数y=-x2+2x-k+1,当x取一切实数时,函数值y恒为负值,即可得△=22-4×(-1)×(-k+1)<0,继而求得答案.
解答:解:∵y=x2-2x+k-1,当x取一切实数时,函数值y恒为正值,
∴△=(-2)2-4×1×(k-1)<0,
解得:k>2,
∴k的取值范围是k>2.
故答案为:k>2.
∴△=(-2)2-4×1×(k-1)<0,
解得:k>2,
∴k的取值范围是k>2.
故答案为:k>2.
点评:此题考查了抛物线与x轴的交点问题.此题难度不大,注意掌握二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
已知方程组
的解是
,则m、n之间的数量关系是( )
|
|
| A、m-16n=5 |
| B、m-16n=11 |
| C、m+16n=-11 |
| D、m+16n=-5 |
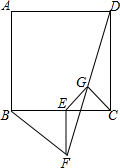 已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点E在BC上,取DF的中点G,连结EG、CG.
已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点E在BC上,取DF的中点G,连结EG、CG.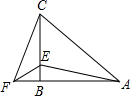 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.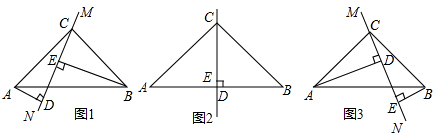
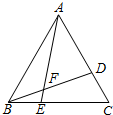 已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB=
已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB= 如图,已知D、E分别是△ABC中AB、AC边上的点,DE∥BC且
如图,已知D、E分别是△ABC中AB、AC边上的点,DE∥BC且