题目内容
7．
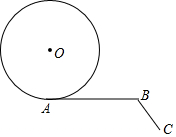如图，已知∠ABC=120°，AB=πr，BC=$\frac{πr}{2}$，半径为r的⊙O从点A出发，沿A→B→C方向滚动到点C时停止，则圆心O运动的路程是$\frac{11}{6}$πr．
分析 圆心O运动的路程分三部分：⊙O从点A出发到与到点B，再以B点为圆心，r为半径旋转60°，然后运动到C点，利用矩形的性质，根据弧长公式求三段的和即可．
解答 
解：如图所示，圆心O运动的路径为线段OD，$\widehat{DE}$，线段EF，
∵AB=πr，BC=$\frac{πr}{2}$，
∴OD=πr，EF=$\frac{πr}{2}$，
∵∠ABC=120°，∠ABD=∠CBE=90°，
∴∠DBE=60°，
∴$\widehat{DE}$=$\frac{60×πr}{180}$=$\frac{1}{3}π$r，
∴圆心O运动的路程=OD+$\widehat{DE}$+EF=πr+$\frac{1}{3}π$r+$\frac{πr}{2}$=$\frac{11}{6}$πr，
故答案为：$\frac{11}{6}$πr．
点评 本题考查了弧长的计算，找到运动轨迹，将运动轨迹划分为三部分进行计算是解题的关键．弧长公式为：l=$\frac{nπR}{180}$（弧长为l，圆心角度数为n，圆的半径为R）．在弧长的计算公式中，n是表示1°的圆心角的倍数，n和180都不要带单位．
练习册系列答案
相关题目
在一条不完整的数轴上从左到右有点A，B，C，其中AB=2，BC=1，如图所示，设点A，B，C所对应数的和是p．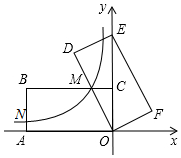
如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上，点B在第二象限．将矩形OABC绕点O顺时针旋转，使点B落在y轴上，得到矩形ODEF，BC与OD相交于点M．若经过点M的反比例函数y=$\frac{k}{x}$（x＜0）的图象交AB于点N，S矩形OABC=32，tan∠DOE=$\frac{1}{2}$，则BN的长为3．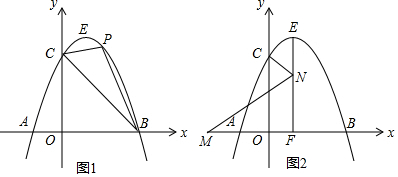
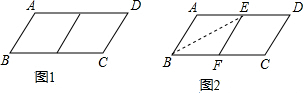2．
在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（ ）
在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（ ）| A． | （$\frac{3}{2}$，0） | B． | （2，0） | C． | （$\frac{5}{2}$，0） | D． | （3，0） |
邻边不相等的平行四边形纸片，减去一个菱形，余下一个四边形，称为第一次操作，在余下的四边形纸片中再剪去一个菱形，余下一个四边形，称为第二次操作，…依此类推，若第n次余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，平行四边形ABCD中，若AB=1，BC=2，则平行四边形ABCD为1阶准菱形．
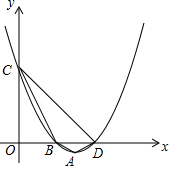已知二次函数y=x2-（a-1）x+a-2，其中a是常数．