题目内容
19．
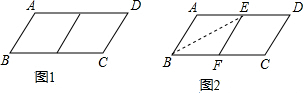邻边不相等的平行四边形纸片，减去一个菱形，余下一个四边形，称为第一次操作，在余下的四边形纸片中再剪去一个菱形，余下一个四边形，称为第二次操作，…依此类推，若第n次余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，平行四边形ABCD中，若AB=1，BC=2，则平行四边形ABCD为1阶准菱形．（1）理解与判断：
①邻边长分别为1和3的平行四边形是2阶准菱形．
②如图2，把平行四边形ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F，得到四边形ABFE，四边形ABFE的形状一定是菱形．若AB=2，AD=3，则图2中的平行四边形ABCD是2阶准菱形．
（2）操作、探究、计算：
①已知某平行四边形的边长分别为2，a（a＞2）且是3阶准菱形，请画出平行四边形ABCD及裁剪线的所有可能示意图，并在图形下方写出a的值．
②已知平行四边形ABCD是一个2017阶准菱形，其邻边长分别为1，m（1＜m＜2），请直接写出m的最大值是2018．
分析 （1）①根据邻边长分别为1和3的平行四边形经过两次操作，即可得出所剩四边形是菱形，即可得出答案；
②根据平行四边形的性质得出AE∥BF，进而得出AE=BF，即可得出答案；根据邻边长分别为2和3的平行四边形经过两次操作，即可得出所剩四边形是菱形，即可得出答案；
（2））①利用3阶准菱形的定义，分四种情形作出图形即可得出答案；
②画出图形即可得到m的最大值；
解答 解：（1）解：（1）①利用邻边长分别为1和3的平行四边形经过两次操作，所剩四边形是边长为1的菱形，
故邻边长分别为1和3的平行四边形是2阶准菱形；
故答案为：2；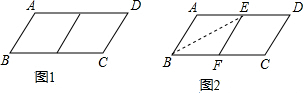
②由折叠知：∠ABE=∠FBE，AB=BF，
∵四边形ABCD是平行四边形，
∴AE∥BF，
∴∠AEB=∠FBE，
∴∠AEB=∠ABE，
∴AE=AB，
∴AE=BF，
∴四边形ABFE是平行四边形，
∴四边形ABFE是菱形；
利用邻边长分别为2和3的平行四边形经过两次操作，所剩四边形是边长为1的菱形，
故邻边长分别为2和3的平行四边形是2阶准菱形；
故答案为：菱形，2；
（2）①答案如图所示：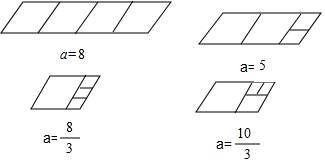
②观察图象可知m的最大值为2017+1=2018．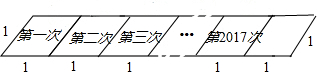
故答案为2018．
点评 此题主要考查了图形的剪拼以及菱形的判定，根据已知n阶准菱形定义正确将平行四边形分割是解题关键，学会用分类讨论的思想思考问题，属于中考压轴题．
练习册系列答案
相关题目
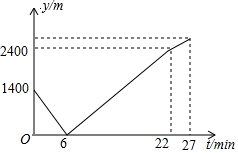小东家与学校之间是一条笔直的公路，早饭后，小东步行前往学校，途中发现忘带画板，停下给妈妈打电话，妈妈接到电话后，带上画板马上赶往学校，同时小东沿原路返回，两人相遇后，小东立即赶往学校，妈妈沿原路返回16min到家，再过5min小东到达学校，小东始终以100m/min的速度步行，小东和妈妈的距离y（单位：m）与小东打完电话后的步行时间t（单位：min）之间的函数关系如图所示，下列四种说法：
17．如图，将一张四边形纸片沿直线剪开，如果剪开后的两个图形的内角和相等，下列四种剪法中，符合要求的是（ ）
| A． | ①② | B． | ①③ | C． | ②④ | D． | ③④ |
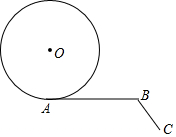如图，已知∠ABC=120°，AB=πr，BC=$\frac{πr}{2}$，半径为r的⊙O从点A出发，沿A→B→C方向滚动到点C时停止，则圆心O运动的路程是$\frac{11}{6}$πr．
14．化简$\frac{a}{a-b}$-$\frac{b}{a+b}$的结果是（ ）
| A． | $\frac{{a}^{2}{+b}^{2}}{{a}^{2}{-b}^{2}}$ | B． | $\frac{{（a+b）}^{2}}{{a}^{2}{-b}^{2}}$ | C． | $\frac{{a}^{2}{-b}^{2}}{{a}^{2}{+b}^{2}}$ | D． | $\frac{{a}^{2}{+b}^{2}}{{（a-b）}^{2}}$ |
