题目内容
2. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )| A. | ($\frac{3}{2}$,0) | B. | (2,0) | C. | ($\frac{5}{2}$,0) | D. | (3,0) |
分析 过点B作BD⊥x轴于点D,易证△ACO≌△BCD(AAS),从而可求出B的坐标,进而可求出反比例函数的解析式,根据解析式与A的坐标即可得知平移的单位长度,从而求出C的对应点.
解答 解:过点B作BD⊥x轴于点D,
∵∠ACO+∠BCD=90°,
∠OAC+∠ACO=90°,
∴∠OAC=∠BCD,
在△ACO与△BCD中,
$\left\{\begin{array}{l}{∠OAC=∠BCD}\\{∠AOC=∠BDC}\\{AC=BC}\end{array}\right.$
∴△ACO≌△BCD(AAS)
∴OC=BD,OA=CD,
∵A(0,2),C(1,0)
∴OD=3,BD=1,
∴B(3,1),
∴设反比例函数的解析式为y=$\frac{k}{x}$,
将B(3,1)代入y=$\frac{k}{x}$,
∴k=3,
∴y=$\frac{3}{x}$,
∴把y=2代入y=$\frac{3}{x}$,
∴x=$\frac{3}{2}$,
当顶点A恰好落在该双曲线上时,
此时点A移动了$\frac{3}{2}$个单位长度,
∴C也移动了$\frac{3}{2}$个单位长度,
此时点C的对应点C′的坐标为($\frac{5}{2}$,0)
故选(C)
点评 本题考查反比例函数的综合问题,涉及全等三角形的性质与判定,反比例函数的解析式,平移的性质等知识,综合程度较高,属于中等题型.

练习册系列答案
相关题目
12. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )| A. | 以点F为圆心,OE长为半径画弧 | B. | 以点F为圆心,EF长为半径画弧 | ||
| C. | 以点E为圆心,OE长为半径画弧 | D. | 以点E为圆心,EF长为半径画弧 |
10.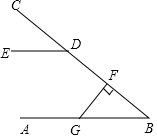 如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
 如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
17.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )


| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
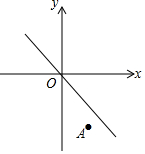 如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).
如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).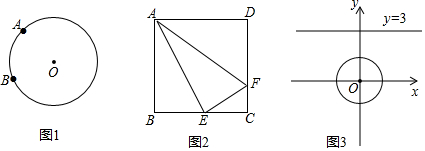
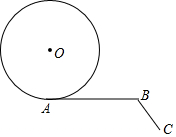 如图,已知∠ABC=120°,AB=πr,BC=$\frac{πr}{2}$,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止,则圆心O运动的路程是$\frac{11}{6}$πr.
如图,已知∠ABC=120°,AB=πr,BC=$\frac{πr}{2}$,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止,则圆心O运动的路程是$\frac{11}{6}$πr.