题目内容
5.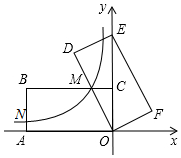 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=$\frac{k}{x}$(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=$\frac{1}{2}$,则BN的长为3.
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=$\frac{k}{x}$(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=$\frac{1}{2}$,则BN的长为3.
分析 利用矩形的面积公式得到AB•BC=32,再根据旋转的性质得AB=DE,OD=OA,接着利用正切的定义得到an∠DOE=$\frac{DE}{OD}$=$\frac{1}{2}$,所以DE•2DE=32,解得DE=4,于是得到AB=4,OA=8,同样在Rt△OCM中利用正切定义得到MC=2,则M(-2,4),易得反比例函数解析式为y=-$\frac{8}{x}$,然后确定N点坐标,最后计算BN的长.
解答 解:∵S矩形OABC=32,
∴AB•BC=32,
∵矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,
∴AB=DE,OD=OA,
在Rt△ODE中,tan∠DOE=$\frac{DE}{OD}$=$\frac{1}{2}$,即OD=2DE,
∴DE•2DE=32,解得DE=4,
∴AB=4,OA=8,
在Rt△OCM中,∵tan∠COM=$\frac{MC}{OC}$=$\frac{1}{2}$,
而OC=AB=4,
∴MC=2,
∴M(-2,4),
把M(-2,4)代入y=$\frac{k}{x}$得k=-2×4=-8,
∴反比例函数解析式为y=-$\frac{8}{x}$,
当x=-8时,y=-$\frac{8}{-8}$=1,则N(-8,1),
∴BN=4-1=3.
故答案为3.
点评 本题考查了旋转图形的坐标:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.也考查了反比例函数图象上点的坐标特征和解直角三角形.

练习册系列答案
相关题目
20. 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )
 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )| A. |  | B. |  | C. |  | D. |  |
10.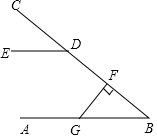 如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
 如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
17.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )


| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
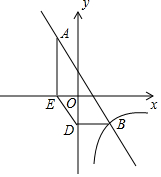 已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.
已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.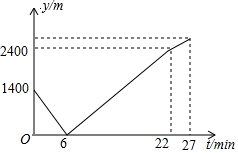 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法: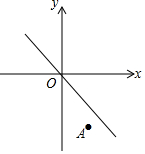 如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).
如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).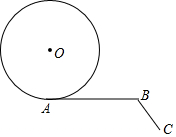 如图,已知∠ABC=120°,AB=πr,BC=$\frac{πr}{2}$,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止,则圆心O运动的路程是$\frac{11}{6}$πr.
如图,已知∠ABC=120°,AB=πr,BC=$\frac{πr}{2}$,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止,则圆心O运动的路程是$\frac{11}{6}$πr.