题目内容
16. 已知二次函数y=x2-(a-1)x+a-2,其中a是常数.
已知二次函数y=x2-(a-1)x+a-2,其中a是常数.(1)求证:不论a为何值,该二次函数的图象与x轴一定有公共点;
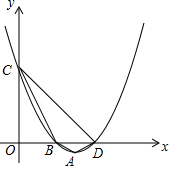
(2)当a=4时,该二次函数的图象顶点为A,与x轴交于B,D两点,与y轴交于C点,求四边形ABCD的面积.
分析 (1)利用根的判别式符号进行证明;
(2)由抛物线解析式求得点B、C、D的坐标,然后利用分割法来求四边形ABCD的面积.
解答 (1)证明:y=x2-(a-1)x+a-2.
因为[-(a-1)]2-4(a-2)=(a-3)2≥0.
所以,方程x2-(a-1)x+a-2=0有实数根.
所以,不论a为何值,该函数的图象与x轴总有公共点;
(2)由题可知:当a=4时,y=x2-3x+2,
因为y=x2-3x+2=(x-$\frac{3}{2}$)2-$\frac{1}{4}$,所以A($\frac{3}{2}$,-$\frac{1}{4}$),
当y=0时,x2-3x+2=0,解得x1=1,x2=2,所以B(1,0),D(2,0),
当x=0时,y=2,所以C(0,2),
所以S四边形ABCD=S△ABD+S△BDC=$\frac{1}{8}$+1=$\frac{9}{8}$.
点评 本题考查了待定系数法,抛物线和坐标轴的交点、顶点坐标,四边形的面积的求法等,(2)利用分割法求四边形的面积是本题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
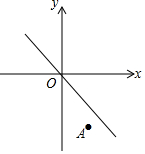 如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).
如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).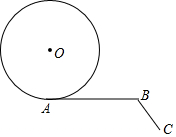 如图,已知∠ABC=120°,AB=πr,BC=$\frac{πr}{2}$,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止,则圆心O运动的路程是$\frac{11}{6}$πr.
如图,已知∠ABC=120°,AB=πr,BC=$\frac{πr}{2}$,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止,则圆心O运动的路程是$\frac{11}{6}$πr.
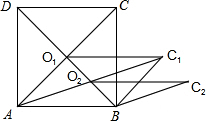 如图,正方形ABCD的面积为2$\sqrt{5}$cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为$\frac{\sqrt{5}}{{2}^{5}}$cm2.
如图,正方形ABCD的面积为2$\sqrt{5}$cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为$\frac{\sqrt{5}}{{2}^{5}}$cm2.