题目内容
14. 如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.则sin∠E的值为( )
如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.则sin∠E的值为( )| A. | $\frac{7}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{14}{25}$ | D. | $\frac{24}{25}$ |
分析 根据∠E=∠CBG,可以把求sin∠E的值得问题转化为求sin∠CBG,进而转化为求Rt△BCG中,由三角函数的定义即可得出结果.
解答 解:连接CD、BG.如图所示: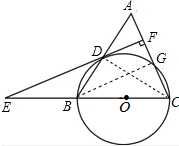
∵BC是直径,
∴∠BDC=90°,CD⊥AB,
∵AC=BC=10,
∴BD=AD=$\frac{1}{2}$AB=6,
∴CD=,$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
∵AB•CD=2S△ABC=AC•BG,
∴BG=$\frac{AB•CD}{AC}$=$\frac{12×8}{10}$=$\frac{48}{5}$,
∴CG=$\sqrt{B{C}^{2}-B{G}^{2}}$=$\frac{14}{5}$.
∵BG⊥AC,DF⊥AC,
∴BG∥EF.
∴∠E=∠CBG,
∴sin∠E=sin∠CBG=$\frac{CG}{BC}$=$\frac{\frac{14}{5}}{10}$=$\frac{7}{25}$;
故选:A.
点评 本题考查了圆周角定理、等腰三角形的性质、勾股定理、三角函数、平行线的判定与性质等知识;熟练掌握圆周角定理,由勾股定理求出CG是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
2. 某男子篮球国家队为备战“第十八届男蓝世锦赛”,选拔一名“得分后卫”,队里这个位置上的人选有甲、乙二人,两个队员在教练规定的5个定点进行投篮比赛(这5个定点到篮筐距离均相等),每个定点投篮10次,现对每个定点的进球个数进行统计,小刚依据统计数据绘制了如图所示尚不完整的统计图表.
某男子篮球国家队为备战“第十八届男蓝世锦赛”,选拔一名“得分后卫”,队里这个位置上的人选有甲、乙二人,两个队员在教练规定的5个定点进行投篮比赛(这5个定点到篮筐距离均相等),每个定点投篮10次,现对每个定点的进球个数进行统计,小刚依据统计数据绘制了如图所示尚不完整的统计图表.
(1)观察球员乙投篮进球数的扇形统计图(图1),回答:
①乙球员5个定点投篮进球数的众数是7,中位数是7;
②进球数为7的扇形所对的圆心角是216°
(2)a=7,$\overline{x{\;}_{乙}}$=7.
(3)请完成图2中表示乙成绩变化情况的折线图;
(4)①观察图2,可以看出乙的成绩比较稳定(填“甲”或“乙”),计算乙成绩的方差,并验证你的判断.
②请你从平均数的方差的角度分析,谁将被选中.
 某男子篮球国家队为备战“第十八届男蓝世锦赛”,选拔一名“得分后卫”,队里这个位置上的人选有甲、乙二人,两个队员在教练规定的5个定点进行投篮比赛(这5个定点到篮筐距离均相等),每个定点投篮10次,现对每个定点的进球个数进行统计,小刚依据统计数据绘制了如图所示尚不完整的统计图表.
某男子篮球国家队为备战“第十八届男蓝世锦赛”,选拔一名“得分后卫”,队里这个位置上的人选有甲、乙二人,两个队员在教练规定的5个定点进行投篮比赛(这5个定点到篮筐距离均相等),每个定点投篮10次,现对每个定点的进球个数进行统计,小刚依据统计数据绘制了如图所示尚不完整的统计图表. | 球员甲、乙进球成绩统计表 | |||||
| 定点A | 定点B | 定点C | 定点D | 定点E | |
| 球员甲成绩 | 8 | 6 | 7 | 4 | 10 |
| 球员乙成绩 | 7 | 8 | 7 | 6 | a |
| 小刚的计算结果 | ||
| 平均数 | 方差 | |
| 球员甲 | 7 | 4 |
①乙球员5个定点投篮进球数的众数是7,中位数是7;
②进球数为7的扇形所对的圆心角是216°
(2)a=7,$\overline{x{\;}_{乙}}$=7.
(3)请完成图2中表示乙成绩变化情况的折线图;
(4)①观察图2,可以看出乙的成绩比较稳定(填“甲”或“乙”),计算乙成绩的方差,并验证你的判断.
②请你从平均数的方差的角度分析,谁将被选中.
 如图,抛物线y=-x2+bx+c交x轴于A(-1,0),B(3,0)两点,交y轴于点C,过点C作x轴的平行线与抛物线交于点D.
如图,抛物线y=-x2+bx+c交x轴于A(-1,0),B(3,0)两点,交y轴于点C,过点C作x轴的平行线与抛物线交于点D.
 A、B两村之间隔一条河,现在要在河上架一座桥.
A、B两村之间隔一条河,现在要在河上架一座桥. 如图,已知△ABC和△ADE都是等腰直角三角形,点D在AC上,M为EC的中点.
如图,已知△ABC和△ADE都是等腰直角三角形,点D在AC上,M为EC的中点. 如图,在等边三角形ABC中,BD是AC边上的中线,延长BC到E,使CE=CD.问:
如图,在等边三角形ABC中,BD是AC边上的中线,延长BC到E,使CE=CD.问: 如图,正方形ABCD的面积为4,AD∥x轴,AB、BC分别交x轴、y轴于点M、N,反比例函数y=$\frac{k}{x}$过点D,若MN+0M=AM,则k的值为2.
如图,正方形ABCD的面积为4,AD∥x轴,AB、BC分别交x轴、y轴于点M、N,反比例函数y=$\frac{k}{x}$过点D,若MN+0M=AM,则k的值为2.