��Ŀ����
16����֪�ı���ABCD�����Ϊ1��OΪ�ı���ABCD�ڵ�һ�㣮��1����ͼ1���ֱ���O����ڵ�A��B��C��D�ĶԳƵ㣬��Ӧ��ΪA�䡢B�䡢C�䡢D�䣬���ı���A��B��C��D������Ϊ4��
��2����ͼ2��E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬�ֱ���O����ڵ�E��F��G��H�ĶԳƵ㣬��Ӧ��ΪE�䡢F�䡢G�䡢H�䣬���ı���EFGH�����Ϊ$\frac{1}{2}$���ı���E��F��G��H������Ϊ2��
��3����ͼ3����E��F��G��H�ֱ���AB��BC��CD��DA���ϵĵ㣬��$\frac{AE}{AB}$=$\frac{BF}{BC}$=$\frac{CG}{CD}$=$\frac{DH}{DA}$=$\frac{1}{x}$������ͼ3�зֱ���O����ڵ�E��F��G��H�ĶԳƵ㣨������ͼ�ۼ�������Ӧ��E��F��G��H�䣬���ú�x�Ĵ���ʽ��ʾ�ı���E��F��G��H������Ϊ$\frac{4{x}^{2}-8x+8}{{x}^{2}}$��
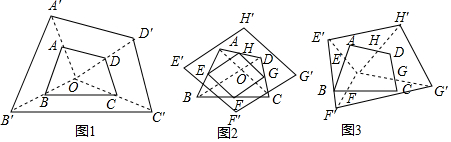
���� ��1��������������λ�߶������ɵ�$\frac{AB}{A'B'}$=$\frac{1}{2}$���ٸ����ı���ABCD���ı���A'B'C'D'��λ��ͼ�Σ���λ�Ʊ�Ϊ$\frac{1}{2}$�����ɵõ�S�ı���A��B��C��D��=1��4=4��
��2������BD��BH������E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬�ɵ�S��AEH=$\frac{1}{2}$S��ABH=$\frac{1}{2}$��$\frac{1}{2}$S��ABD=$\frac{1}{4}$S��ABD ��S��CFG=$\frac{1}{4}$S��CBD ��S��DHG+S��BEF=$\frac{1}{4}$S�ı���ABCD �������õ�S�ı���EFGH=��1-$\frac{1}{4}$��2��S�ı���ABCD=$\frac{1}{2}$��1=$\frac{1}{2}$���ٸ��ݣ�1���н��ۿ�֪��S�ı���E��F��G��H��=4S�ı���EFGH=4��$\frac{1}{2}$=2��
��3�����ã�2���еķ����������S�ı���EFGH=$\frac{{x}^{2}-2x+2}{{x}^{2}}$���ٸ���S�ı���E��F��G��H��=4S�ı���EFGH���м��㼴�ɣ�
���  �⣺��1�����ݶԳ��Կɵã���A��OA'���е㣬��BʱOB'���е㣬
�⣺��1�����ݶԳ��Կɵã���A��OA'���е㣬��BʱOB'���е㣬
��AB�ǡ�A'B'O����λ�ߣ�
��$\frac{AB}{A'B'}$=$\frac{1}{2}$��
����ɵã��ı���ABCD���ı���A'B'C'D'��λ��ͼ�Σ���λ�Ʊ�Ϊ$\frac{1}{2}$��
���ı���A��B��C��D�����������ı���ABCD�������4����
��S�ı���A��B��C��D��=1��4=4��
�ʴ�Ϊ��4��
��2����ͼ2������BD��BH��
��E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬
��S��AEH=$\frac{1}{2}$S��ABH=$\frac{1}{2}$��$\frac{1}{2}$S��ABD=$\frac{1}{4}$S��ABD ��
ͬ����S��CFG=$\frac{1}{4}$S��CBD ��
��S��AEH+S��CFG=$\frac{1}{4}$��S��ABD+S��CBD��=$\frac{1}{4}$S�ı���ABCD ��
ͬ���ɵã�S��DHG+S��BEF=$\frac{1}{4}$S�ı���ABCD ��
��S�ı���EFGH=��1-$\frac{1}{4}$��2��S�ı���ABCD=$\frac{1}{2}$��1=$\frac{1}{2}$��
�ɣ�1����֪��S�ı���E��F��G��H��=4S�ı���EFGH=4��$\frac{1}{2}$=2��
�ʴ�Ϊ��$\frac{1}{2}$��2��
��3����ͼ3����E�䣬F�䣬G�䣬H�伴Ϊ����
��ͼ4������EF��FG��GH��HE������BD��BH��
��$\frac{AE}{AB}$=$\frac{BF}{BC}$=$\frac{CG}{CD}$=$\frac{DH}{DA}$=$\frac{1}{x}$��
��S��AEH=$\frac{1}{x}$S��ABH=$\frac{1}{x}$��$\frac{x-1}{x}$S��ABD=$\frac{x-1}{{x}^{2}}$S��ABD ��
ͬ����S��CFG=$\frac{x-1}{{x}^{2}}$S��CBD ��
��S��AEH+S��CFG=$\frac{x-1}{{x}^{2}}$��S��ABD+S��CBD��=$\frac{x-1}{{x}^{2}}$S�ı���ABCD ��
ͬ���ɵã�S��DHG+S��BEF=$\frac{x-1}{{x}^{2}}$S�ı���ABCD ��
��S�ı���EFGH=��1-$\frac{x-1}{{x}^{2}}$��2��S�ı���ABCD=$\frac{{x}^{2}-2x+2}{{x}^{2}}$��1=$\frac{{x}^{2}-2x+2}{{x}^{2}}$��
�ɣ�1����֪��S�ı���E��F��G��H��=4S�ı���EFGH=4��$\frac{{x}^{2}-2x+2}{{x}^{2}}$=$\frac{4{x}^{2}-8x+8}{{x}^{2}}$��
�ʴ�Ϊ��$\frac{4{x}^{2}-8x+8}{{x}^{2}}$��
���� ������Ҫ�������е��ı����Լ�λ��ͼ�ε����ʵ����ã��������Ĺؼ��ǽ�ͼ�ν��зָ���õȵȸߵ������ε�����Ⱦ͵��ڶ�Ӧ�ıȽ��м��㣮����ʱע�⣺���ƶ���ε����֮�ȵ������Ʊȵ�ƽ����

 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д� С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д�| A�� | 2��3 | B�� | 8��5 | C�� | 10��1 | D�� | 5��8 |
| A�� | $\sqrt{-x-2}$ | B�� | $\sqrt{x}$ | C�� | $\sqrt{{x}^{2}+2}$ | D�� | $\sqrt{-5}$ |
| A�� | 2x+1=0 | B�� | y2+x=0 | C�� | x2-x=0 | D�� | $\frac{1}{x}$+x2=0 |
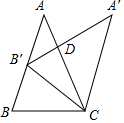 ��ͼ���ڡ�ABC�У�AB=AC������ABC�Ƶ�C˳ʱ����ת��õ���A'B'C�����A'CB=a����B'��AB�ϣ����ADA'=4��-360�㣨�ú�a��ʽ�ӱ�ʾ��
��ͼ���ڡ�ABC�У�AB=AC������ABC�Ƶ�C˳ʱ����ת��õ���A'B'C�����A'CB=a����B'��AB�ϣ����ADA'=4��-360�㣨�ú�a��ʽ�ӱ�ʾ�� ��ͼ����ƽ��ֱ������ϵ�У�����������y=2x�뷴��������y=$\frac{k}{x}$��k��0���ཻ��A��B���㣬��֪��A�������ǣ�1��a��������һ�κ���y=mx+n��m��0����ͼ����A����x���ڵ�C����y���ڵ�D��OC=$\sqrt{5}$OA��
��ͼ����ƽ��ֱ������ϵ�У�����������y=2x�뷴��������y=$\frac{k}{x}$��k��0���ཻ��A��B���㣬��֪��A�������ǣ�1��a��������һ�κ���y=mx+n��m��0����ͼ����A����x���ڵ�C����y���ڵ�D��OC=$\sqrt{5}$OA��