题目内容
19.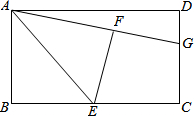 在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,猜想线段GF与GC有何数量关系?并证明你的结论.
在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,猜想线段GF与GC有何数量关系?并证明你的结论.
分析 连接EG,由翻折的性质可知:BE=EF,∠B=∠AFE=90°,然后证明Rt△EFG≌Rt△ECG即可.
解答 解:连接EG.
由翻折的性质可知:BE=EF,∠B=∠AFE=90°.
∴∠EFG=∠C=90°.
∵E是BC的中点,
∴BE=EC.
∴EF=EC.
在Rt△EFG和Rt△ECG中,$\left\{\begin{array}{l}{EF=EC}\\{EG=EG}\end{array}\right.$,
∴Rt△EFG≌Rt△ECG.
∴FG=GC.
点评 本题主要考查的是翻折的性质、全等三角形的性质和判定,证得Rt△EFG≌Rt△ECG是解题的关键.

练习册系列答案
相关题目
7. 如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,在平面直角坐标系中,直线CD与x轴、y轴分别交于点C,D,与反比例函数y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于E,F.过点E作EA⊥y轴于A,过点F作FB⊥x轴于B,直线EA与FB交于点G.若$\frac{DE}{DF}$=$\frac{1}{4}$,记△GEF的面积为S1,△OEF的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
4.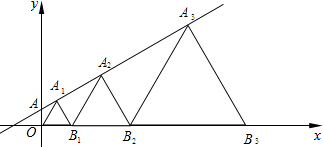 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )| A. | ($\frac{\sqrt{3}}{3}$)9 | B. | ($\frac{\sqrt{3}}{3}$)10 | C. | 29•$\sqrt{3}$ | D. | 210•$\sqrt{3}$ |
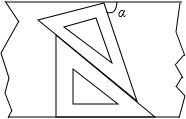 如图,一副三角板放置在两边互相平行的纸板上,其中下面部分是含45°角的三角板上,上面部分是一个含30°角的三角板,则图中∠α的度数是75°.
如图,一副三角板放置在两边互相平行的纸板上,其中下面部分是含45°角的三角板上,上面部分是一个含30°角的三角板,则图中∠α的度数是75°.