��Ŀ����
7�� ��ͼ����ƽ��ֱ������ϵ�У�ֱ��CD��x�ᡢy��ֱ��ڵ�C��D���뷴��������y=$\frac{k}{x}$��kΪ��������k��0���ڵ�һ����ͼ����E��F������E��EA��y����A������F��FB��x����B��ֱ��EA��FB���ڵ�G����$\frac{DE}{DF}$=$\frac{1}{4}$���ǡ�GEF�����ΪS1����OEF�����ΪS2����$\frac{{S}_{1}}{{S}_{2}}$=��������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��CD��x�ᡢy��ֱ��ڵ�C��D���뷴��������y=$\frac{k}{x}$��kΪ��������k��0���ڵ�һ����ͼ����E��F������E��EA��y����A������F��FB��x����B��ֱ��EA��FB���ڵ�G����$\frac{DE}{DF}$=$\frac{1}{4}$���ǡ�GEF�����ΪS1����OEF�����ΪS2����$\frac{{S}_{1}}{{S}_{2}}$=��������| A�� | $\frac{1}{4}$ | B�� | $\frac{3}{5}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{5}{8}$ |
���� ����E��F���ڷ�����������ͼ���ϵó������E��F�����꣬�����ֱ�ó���GEF�����S1�Լ���OEF�����S2��Ȼ�ɵó��𰸣�
���  �⣺����F��FR��AO�ڵ�R��EW��BO�ڵ�W��
�⣺����F��FR��AO�ڵ�R��EW��BO�ڵ�W��
��$\frac{DE}{DF}$=$\frac{1}{4}$��
��$\frac{AE}{FR}$=$\frac{1}{4}$��
��AE•EW=FR•BF��
��$\frac{AE}{FR}$=$\frac{FB}{EW}$=$\frac{1}{4}$��
��S1=$\frac{1}{2}$��4x-x����4y-y��=$\frac{9}{2}$xy��
��E����������x��4y������F����������4x��y����
�ߡ�OEF�����Ϊ��S2=S����GBOA-S1-S��AEO-S��FOB
=GB•OB-$\frac{9}{2}$xy-$\frac{1}{2}$AE•AO-$\frac{1}{2}$FB•BO
=4x•4y-$\frac{9}{2}$xy-$\frac{1}{2}$x•4y-$\frac{1}{2}$y•4x
=16xy-$\frac{9}{2}$xy-4xy
=$\frac{15}{2}$xy
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\frac{9}{2}xy}{\frac{15}{2}xy}$=$\frac{3}{5}$��
��ѡ��B��
���� ������Ҫ�����˷������������ۺ�Ӧ���Լ������������������֪��ʾ��E��F�ĵ������ǽ���ؼ����ѶȽϴ�Ҫ��ͬѧ���ܽ���ѧ��֪ʶ�ڻ��ͨ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�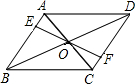 ��ͼ���ı���ABCD�У�EF���Խ��߽��㣬��OB+BE=OD+DF����OE=OF��֤���ı���ABCDΪƽ���ı��Σ�
��ͼ���ı���ABCD�У�EF���Խ��߽��㣬��OB+BE=OD+DF����OE=OF��֤���ı���ABCDΪƽ���ı��Σ�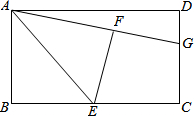 �ھ���ABCD�У�E��BC���е㣬����ABE��AE�۵���õ���AFE����F�ھ���ABCD�ڲ����ӳ�AF��CD�ڵ�G�������߶�GF��GC�к�������ϵ����֤����Ľ��ۣ�
�ھ���ABCD�У�E��BC���е㣬����ABE��AE�۵���õ���AFE����F�ھ���ABCD�ڲ����ӳ�AF��CD�ڵ�G�������߶�GF��GC�к�������ϵ����֤����Ľ��ۣ�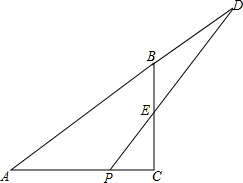 ��ͼ����Rt��ABC�У���ACB=90�㣬AB=10��BC��AC=3��4����D��AB�ӳ����ϣ�BD=6����P��AC�ϵ�-�����㣮PD��BC�ڵ�E����PC=x��S��PCE=y��
��ͼ����Rt��ABC�У���ACB=90�㣬AB=10��BC��AC=3��4����D��AB�ӳ����ϣ�BD=6����P��AC�ϵ�-�����㣮PD��BC�ڵ�E����PC=x��S��PCE=y��