题目内容
8.在△ABC中,AB=AC,D是边AC上的一点,E是边AB上的一点,联结BD、DE,已知AD=BD=BE=BC,写出该图形中的所有相似三角形,并简要说明理由.分析 如图,设∠A=x,根据等腰三角形的性质和三角形内角和定理可得∠ABC=∠C=90°-$\frac{1}{2}$x,由AD=BD得到∠1=∠A=x,则∠DBC=90°-$\frac{3}{2}$x,接着由BD=BC得到∠2=∠C=90°-$\frac{1}{2}$x,于是根据三角形内角和定理可得90°-$\frac{3}{2}$x+90°-$\frac{1}{2}$x+90°-$\frac{1}{2}$x=180°,解得x=36°,然后计算出图中所有角的度数,再利用有两组角对应相等的两个三角形相似找相似三角形.
解答 解: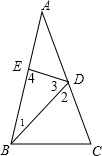 如图,
如图,
设∠A=x,
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-x)=90°-$\frac{1}{2}$x,
∵AD=BD,
∴∠1=∠A=x,
∴∠DBC=90°-$\frac{1}{2}$x-x=90°-$\frac{3}{2}$x,
∵BD=BC,
∴∠2=∠C=90°-$\frac{1}{2}$x,
而∠DBC+∠2+∠C=180°,
∴90°-$\frac{3}{2}$x+90°-$\frac{1}{2}$x+90°-$\frac{1}{2}$x=180°,解得x=36°,
∴∠A=∠1=36°,
∠DBC=90°-$\frac{3}{2}$×36°=36°,
∴∠3=∠4=∠C=∠ABC=72°,
∴△ABC∽△BED∽△BDC.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.有两组角对应相等的两个三角形相似.也考查了等腰三角形的性质和三角形内角和定理.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
18.某下岗职工购进一批货物,到集贸市场零售,已知卖出去的货物数量x与售价y的关系如下表:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当货物数量时5kg的时候,售价是多少元?
(3)如果售价是(27+0.9)元,那么货物数量是多少千克?
(4)你能尝试着写出卖出去的售价y与货物数量x的之间的关系式吗?
| 数量x(千克) | 1 | 2 | 3 | 4 | 5 |
| 售价y(元) | 3+0.1 | 6+0.2 | 9+0.3 | 12+0.4 | 15+0.5 |
(2)当货物数量时5kg的时候,售价是多少元?
(3)如果售价是(27+0.9)元,那么货物数量是多少千克?
(4)你能尝试着写出卖出去的售价y与货物数量x的之间的关系式吗?
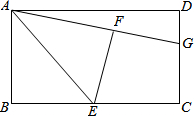 在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,猜想线段GF与GC有何数量关系?并证明你的结论.
在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,猜想线段GF与GC有何数量关系?并证明你的结论.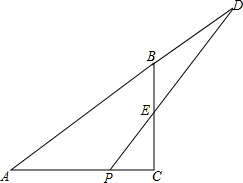 如图.在Rt△ABC中.∠ACB=90°,AB=10,BC:AC=3:4,点D在AB延长线上,BD=6,点P是AC上的-个动点.PD交BC于点E.设PC=x,S△PCE=y.
如图.在Rt△ABC中.∠ACB=90°,AB=10,BC:AC=3:4,点D在AB延长线上,BD=6,点P是AC上的-个动点.PD交BC于点E.设PC=x,S△PCE=y. 如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠OBE的度数.
如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠OBE的度数. 如图:已知AB是⊙O的直径,直线l与⊙O相切于点C,且弦CD⊥AB,垂足为E,BF⊥l,垂足为F,BF交⊙O于G.
如图:已知AB是⊙O的直径,直线l与⊙O相切于点C,且弦CD⊥AB,垂足为E,BF⊥l,垂足为F,BF交⊙O于G.