题目内容
19.一菱形的两条对角线的和为14,面积为24,则此菱形的周长为( )| A. | 12 | B. | 16 | C. | 20 | D. | 28 |
分析 先由已知条件求出2OA•OB=24,OA+OB=7,再根据勾股定理求出AB2=OA2+OB2=(OA+OB)2-2OA•OB,得出AB,即可求出周长.
解答 解:如图所示: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC⊥BD,
∴AC+BD=14,S菱形ABCD=$\frac{1}{2}$AC•BD=2OA•OB=24,
∴OA+OB=7,
∴AB2=OA2+OB2=(OA+OB)2-2OA•OB=72-24=25,
∴AB=5,
∴菱形的周长=5×4=20;
故选:C.
点评 本题考查了菱形的性质、面积的计算方法;由已知条件得出OA、OB的和与积的关系求出边长是解决问题的关键.

练习册系列答案
相关题目
4.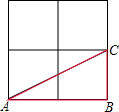 如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
 如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
11.方程x2=2x的解是( )
| A. | x=2 | B. | x1=2,x2=0 | C. | x1=$\sqrt{2}$,x2=0 | D. | x=0 |
9.地球上的海洋面积约为36100000km2,用科学记数法可表示为( )
| A. | 3.61×106km2 | B. | 3.61×107km2 | C. | 0.361×108km2 | D. | 3.61×109km2 |
 如图,已知DE∥BC,EF平分∠DEC,且∠ADE=50°,∠C=80°.
如图,已知DE∥BC,EF平分∠DEC,且∠ADE=50°,∠C=80°. (1)请在图中的网格中画三边长分别为:$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$的格点△ABC(即顶点都在格点上);
(1)请在图中的网格中画三边长分别为:$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$的格点△ABC(即顶点都在格点上); 在三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,则线段AB与DF平行吗?BC与DE平行吗?为什么.
在三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,则线段AB与DF平行吗?BC与DE平行吗?为什么.