题目内容
3.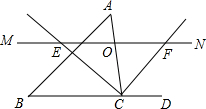 如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
分析 ①根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案;
②当AC⊥BD时,CE=CF;
③根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长;
④根据平行四边形的判定以及矩形的判定得出即可.
解答 解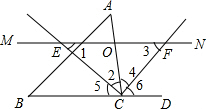 ①∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
①∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
∴①正确;
②当AC⊥BD时,CE=CF;
故②错误;
③∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∴OC=$\frac{1}{2}$EF=6.5;
故③错误;
④当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
故④正确;
故选B.
点评 此题主要考查了矩形的判定、平行四边形的判定和直角三角形的判定等知识,根据已知得出∠ECF=90°是解题关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,在矩形ABCD中,AB=10,BC=5,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为8.
如图,在矩形ABCD中,AB=10,BC=5,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为8. 如图,在平行四边形ABCD中,点E、F分别为AB、BC中点,则三角形BEF与多边形EFCDA的面积之比为1:7.
如图,在平行四边形ABCD中,点E、F分别为AB、BC中点,则三角形BEF与多边形EFCDA的面积之比为1:7.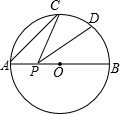 如图,AB是⊙O的直径,AB=2,点C是半圆弧AB上的一点,且∠CAB=40°,点D是BC的中点,点P是直径AB上的动点,则线段PC+PD的最小值是$\sqrt{3}$.
如图,AB是⊙O的直径,AB=2,点C是半圆弧AB上的一点,且∠CAB=40°,点D是BC的中点,点P是直径AB上的动点,则线段PC+PD的最小值是$\sqrt{3}$.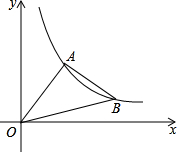 如图,在等腰Rt△ABO中,∠OAB=Rt∠,点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点B在点A的右侧,若点A的横坐标为2,则k的值是2+2$\sqrt{5}$.
如图,在等腰Rt△ABO中,∠OAB=Rt∠,点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点B在点A的右侧,若点A的横坐标为2,则k的值是2+2$\sqrt{5}$.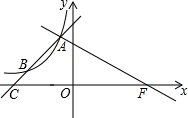 已知反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2).
已知反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2). 如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.