题目内容
4.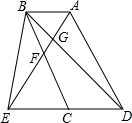 如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE.
如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE.(1)求证:△AFB≌△EFC;
(2)判断CF与AD的关系,并说明理由.
分析 (1)根据平行四边形性质推出AB=CD=CE,AB∥CD,推出∠ABF=FCE,∠BAF=∠FEC,根据全等三角形的判定证出即可;
(2)根据全等三角形的性质解答即可.
解答 (1)证明:在平行四边形ABCD中,
∵AB∥CD,
∴∠BAF=∠CEF,∠ABF=∠ECF,
∵AB=CD,CE=CD,
∴AB=CE,
在△AFB和△EFC中
$\left\{\begin{array}{l}{∠BAF=∠CEF}\\{AB=CE}\\{∠ABF=∠ECF}\end{array}\right.$,
∴△AFB≌△EFC.
(2)CF$\stackrel{∥}{=}$$\frac{1}{2}AD$,
理由如下:∵△AFB≌△EFC,
∴AF=EF,又EC=CD,
∴CF$\stackrel{∥}{=}$$\frac{1}{2}AD$.
点评 本题考查了平行四边形的性质,关键是根据平行线的性质,全等三角形的判定进行推理,题目比较典型,难度也适中.

练习册系列答案
相关题目
16.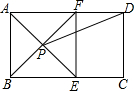 如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF是正方形;
(2)如果AB=4,AD=7,求tan∠ADP的值.
 如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.(1)求证:四边形ABEF是正方形;
(2)如果AB=4,AD=7,求tan∠ADP的值.
9.设a=$\sqrt{2}-1$,b=$\sqrt{5}$-2,c=$\sqrt{10}$-3.则a、b、c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<b<a |
 如图,在矩形ABCD中,AB=10,BC=5,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为8.
如图,在矩形ABCD中,AB=10,BC=5,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为8. 已知反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2).
已知反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2). 如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.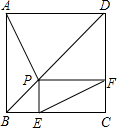 如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F.
如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F.