题目内容

5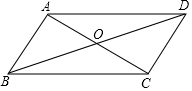．如图，在?ABCD中，∠CAB=90°，OA=1cm，OB=2cm，求AC，AD的长．

分析 根据平行四边形的性质：对角线互相平分由OA的长可以求出AC的长，由勾股定理求出AB2，再由勾股定理求出BC，即可得出AD的长．

解答 解：∵四边形ABCD是平行四边形，
∴AC=2AO=2cm，AD=BC，
∵∠CAB=90°，
∴由勾股定理得：AB2=OB2-OA2=22-12=3，
∴BC=AD=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{3+4}$=$\sqrt{7}$（cm）．

点评 本题主要考查对平行四边形的性质，勾股定理等知识点的理解和掌握；熟练掌握平行四边形的性质，由勾股定理求出AB2是解决问题的关键．

练习册系列答案
相关题目
15．已知抛物线交x轴于A（-1，0），B（3，0），交y轴于C（0，-3），以AB为直径作⊙M，过抛物线上一点P作⊙M的切线PD，切点为D，交⊙M的切线AE于E，连接DM并延长交⊙M于N，连接AN，AD．
（1）求抛物线的函数解析式及顶点坐标；
（2）若S四边形EAMD=4$\sqrt{3}$，求直线PD的函数解析式；
（3）在抛物线上是否存在点P，使S四边形EAMD=S△DAN？若存在，求出P点的坐标；若不存在，说明理由．
16．一块三角形材料如图所示，∠A=30°，∠C=90°，AB=12．用这块材料剪出一个矩形CDEF，其中，点D、E、F分别在BC、AB、AC上（点E与点A、点B均不重合）．设AE=x，矩形CDEF的面积为S．
（1）求出S的函数关系式并直接写出自变量x的取值范围
（2）当x为何值时，S有最大值，并求出S的最大值
（3）当x=18-6$\sqrt{3}$时，矩形CDEF为正方形．
13．如图1，在?ABCD中，对角线AC与BD相交于点O，经过点O的直线与边AB相交于点E，与边CD相交于点F．
（1）求证：OE=OF；
（2）如图2，连接DE，BF，当DE⊥AB时，在不添加其他辅助线的情况下，直接写出腰长等于$\frac{1}{2}$BD的所有的等腰三角形．
20．（1）计算：（$\frac{1}{2}$）-1+|-$\frac{\sqrt{12}}{3}$|-（2-$\sqrt{3}$）0+tan30°
（2）解不等式组$\left\{\begin{array}{l}{\frac{x+3}{2}≥x}\\{3（x-1）＞3}\end{array}\right.$．
10．化简：$\sqrt{12}$=2$\sqrt{3}$；$\sqrt{（5-7）^{2}}$×$\sqrt{（2-6）^{2}}$=8．
17．在△ABC中，∠ACB=90°，AC=BC，点O是AB的中点，点D是AC上一点，过点C作CE⊥BD于点E，连接EO．
（1）过点O作OF⊥OE交BD于点F，如图1，试判断线段OE与OF之间的数量关系，并说明理由．
（2）若点D是AC的中点，BC=4，请在备用图上画出符合条件的图形，并求出OE的长．
（3）若CD=$\frac{1}{3}$AC，BC=6，请直接写出OE的长（不用说理）．
14．如果在四边形内存在一点，它到四个顶点的距离相等，那么这个四边形一定是（　　）
A．平行四边形B．矩形C．正方形D．菱形
15．若关于x的分式方程$\frac{2}{x-3}$-$\frac{x+m}{x-3}$=2有增根，则m的值为-5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网