��Ŀ����
17���ڡ�ABC�У���ACB=90�㣬AC=BC����O��AB���е㣬��D��AC��һ�㣬����C��CE��BD�ڵ�E������EO����1������O��OF��OE��BD�ڵ�F����ͼ1�����ж��߶�OE��OF֮���������ϵ����˵�����ɣ�
��2������D��AC���е㣬BC=4�����ڱ���ͼ�ϻ�������������ͼ�Σ������OE�ij���
��3����CD=$\frac{1}{3}$AC��BC=6����ֱ��д��OE�ij�������˵������
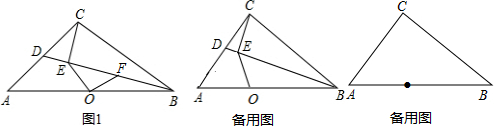
���� ��1�����ۣ�OE=OF����ͼ1�У�����OC����CA=CB����ACB=90�㣬OA=OB���Ƴ�OC=OB��OC��AB����OBC=��BCO=45�㣬ȡBC���е�K������EK��KO����CE��DB���Ƴ���CEB=90�㣬EK=CK=KB=OK���Ƴ�C��E��O��B�ĵ㹲Բ���Ƴ���OEF=$\frac{1}{2}$��OKB���ɴ˼��ɽ�����⣮
��2���ɡ�DCE�ס�DBC����$\frac{CD}{DB}$=$\frac{DE}{DC}$=$\frac{CE}{BC}$�����DE��CE��EB���ɡ�EOC�ա�FOB����CE=BF=$\frac{4\sqrt{5}}{5}$���Ƴ�EF=BE-BF=$\frac{4\sqrt{5}}{5}$����OE=EF•cos45�㼴�ɽ�����⣮
��3���ɡ�DCE�ס�DBC����$\frac{CD}{DB}$=$\frac{DE}{DC}$=$\frac{CE}{BC}$�����DE��CE��EB���ɡ�EOC�ա�FOB����CE=BF�����ݡ���㼴�ɣ�
��� �⣺��1�����ۣ�OE=OF���������£�
��ͼ1�У�����OC��
��CA=CB����ACB=90�㣬OA=OB��
��OC=OB��OC��AB����OBC=��BCO=45�㣬ȡBC���е�K������EK��KO��
��CE��DB��
���CEB=90�㣬EK=CK=KB=OK��
��C��E��O��B�ĵ㹲Բ��
���OEF=$\frac{1}{2}$��OKB��
��OC=OB��CK=KB��
��OK��BC��
���OKB=90�㣬
���OEB=45�㣬
��OE��OF��
���EOF=90�㣬
���OEF=��OFE=45�㣬
��OE=OF��
��2����ͼ2��ʾ������OC��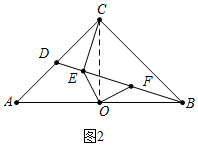
��BC=CA=4��CD=AD=2��
��Rt��DCB��BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
�ߡ�CDE=��CDB����CED=��DCB��
���DCE�ס�DBC��
��$\frac{CD}{DB}$=$\frac{DE}{DC}$=$\frac{CE}{BC}$��
��$\frac{2}{2\sqrt{5}}$=$\frac{DE}{2}$=$\frac{CE}{4}$��
��DE=$\frac{2\sqrt{5}}{5}$��CE=$\frac{4\sqrt{5}}{5}$��
��BE=$\frac{8\sqrt{5}}{5}$��
�ߡ�EOF=��COB=90�㣬
���EOC=��FOB��
�ڡ�EOC�͡�FOB�У�
$\left\{\begin{array}{l}{EO=OF}\\{��EOC=��FOB}\\{OC=OB}\end{array}\right.$��
���EOC�ա�FOB��
��CE=BF=$\frac{4\sqrt{5}}{5}$��
��EF=BE-BF=$\frac{4\sqrt{5}}{5}$��
��OE=EF•cos45��=$\frac{2\sqrt{10}}{5}$��
��3����ͼ3�У�����AC��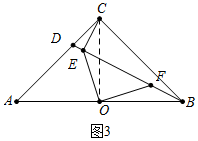
������CD=2��BC=6��BD=2$\sqrt{10}$��
�ߡ�DCE�ס�DBC��
��$\frac{CD}{DB}$=$\frac{DE}{DC}$=$\frac{CE}{BC}$��
��$\frac{2}{2\sqrt{10}}$=$\frac{DE}{2}$=$\frac{EC}{6}$��
��DE=$\frac{\sqrt{10}}{5}$��CE=$\frac{3\sqrt{10}}{5}$��EB=$\frac{9\sqrt{10}}{5}$��
�ߡ�EOC�ա�FOB��
��CE=BF=$\frac{3\sqrt{10}}{5}$��
��EF=EB-BF=$\frac{6\sqrt{10}}{5}$��
��OE=EF•cos45��=$\frac{6\sqrt{5}}{5}$��
���� ���⿼��ȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ�������Ǻ��������ɶ��������������ε��ж������ʡ�Բ��֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬�����п�ѹ���⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�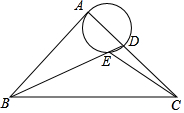 ��ͼ���ڵ���Rt��ABC�У���BAC=90�㣬AB=AC��BC=2$\sqrt{2}$����D��AC����һ���㣬����BD����ADΪֱ����Բ��BD�ڵ�E�����߶�CE���ȵ���СֵΪ��������
��ͼ���ڵ���Rt��ABC�У���BAC=90�㣬AB=AC��BC=2$\sqrt{2}$����D��AC����һ���㣬����BD����ADΪֱ����Բ��BD�ڵ�E�����߶�CE���ȵ���СֵΪ��������| A�� | 2$\sqrt{2}$-2 | B�� | $\sqrt{5}-2$ | C�� | $\sqrt{5}-1$ | D�� | $\sqrt{3}-1$ |
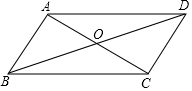 ��ͼ����?ABCD�У���CAB=90�㣬OA=1cm��OB=2cm����AC��AD�ij���
��ͼ����?ABCD�У���CAB=90�㣬OA=1cm��OB=2cm����AC��AD�ij���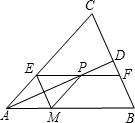 ��ͼ��������ABC�У�AB=AC��ADƽ�֡�BAC��BC��D�����߶�AD����ȡһ��P����A���⣩������P��EF��AB���ֱ�AC��BC��E��F�㣬��PM��AC����AB��M�㣬����ME��
��ͼ��������ABC�У�AB=AC��ADƽ�֡�BAC��BC��D�����߶�AD����ȡһ��P����A���⣩������P��EF��AB���ֱ�AC��BC��E��F�㣬��PM��AC����AB��M�㣬����ME��