题目内容
13.如图1,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线与边AB相交于点E,与边CD相交于点F.(1)求证:OE=OF;
(2)如图2,连接DE,BF,当DE⊥AB时,在不添加其他辅助线的情况下,直接写出腰长等于$\frac{1}{2}$BD的所有的等腰三角形.
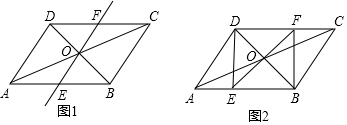
分析 (1)由四边形ABCD是平行四边形,可得OA=OC,AB∥CD,则可证得△AOE≌△COF(ASA),继而证得OE=OF;
(2)证明四边形DEBF是矩形,由矩形的性质和等腰三角形的性质即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,OB=OD,
∴∠OAE=∠OCF,
在△OAE和△OCF中,$\left\{\begin{array}{l}{∠OAE=∠OCF}&{\;}\\{OA=OC}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴OE=OF;
(2)解:∵OE=OF,OB=OD,
∴四边形DEBF是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形DEBF是矩形,
∴BD=EF,
∴OD=OB=OE=OF=$\frac{1}{2}$BD,
∴腰长等于$\frac{1}{2}$BD的所有的等腰三角形为△DOF,△FOB,△EOB,△DOE.
点评 此题考查了平行四边形的性质、全等三角形的判定与性质、矩形的性质、等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
18.2012年,我市参加中考的学生约为33200万人,用科学记数法表示为( )
| A. | 0.332×105人 | B. | 33.2×106人 | C. | 3.32×108人 | D. | 332×108 人 |
3.在-$\sqrt{(-5)^{2}}$,2π,$\sqrt{0.4}$,$\frac{1}{7}$,0中无理数个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,六角螺母的横截面是正六边形,它的每条边都相等,每个内角也都相等.求这个六边形的每一个内角的度数.
如图,六角螺母的横截面是正六边形,它的每条边都相等,每个内角也都相等.求这个六边形的每一个内角的度数.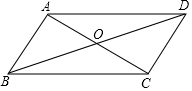 如图,在?ABCD中,∠CAB=90°,OA=1cm,OB=2cm,求AC,AD的长.
如图,在?ABCD中,∠CAB=90°,OA=1cm,OB=2cm,求AC,AD的长.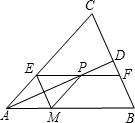 如图,等腰△ABC中,AB=AC,AD平分∠BAC交BC于D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC、BC于E,F点,作PM∥AC,交AB于M点,连接ME.
如图,等腰△ABC中,AB=AC,AD平分∠BAC交BC于D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC、BC于E,F点,作PM∥AC,交AB于M点,连接ME.