题目内容
15.若关于x的分式方程$\frac{2}{x-3}$-$\frac{x+m}{x-3}$=2有增根,则m的值为-5.分析 增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.把增根代入化为整式方程的方程即可求出m的值.
解答 解:方程两边都乘(x-3),得
2-x-m=2(x-3)
∵原方程增根为x=3,
∴把x=3代入整式方程,得m=-1.
点评 本题考查了分式方程的增根,增根确定后可按如下步骤进行:化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值.

练习册系列答案
相关题目
6.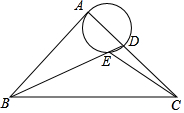 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )| A. | 2$\sqrt{2}$-2 | B. | $\sqrt{5}-2$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{3}-1$ |
3.在-$\sqrt{(-5)^{2}}$,2π,$\sqrt{0.4}$,$\frac{1}{7}$,0中无理数个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.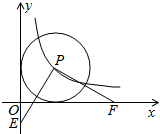 如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
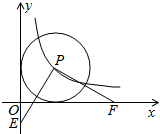 如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )| A. | 6 | B. | 5 | C. | 4 | D. | 2$\sqrt{5}$ |
5.下列说法中正确的是( )
| A. | 单项式x的系数和次数都是零 | B. | 34x3是7次单项式 | ||
| C. | a2b3的系数是5 | D. | 0是单项式 |
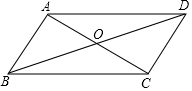 如图,在?ABCD中,∠CAB=90°,OA=1cm,OB=2cm,求AC,AD的长.
如图,在?ABCD中,∠CAB=90°,OA=1cm,OB=2cm,求AC,AD的长.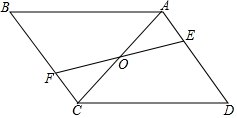 已知:如图,平行四边形 ABCD中,点E、F分别在AD、BC上,且ED=BF,EF与AC相交于点O.
已知:如图,平行四边形 ABCD中,点E、F分别在AD、BC上,且ED=BF,EF与AC相交于点O. 如图,AB∥CD,∠AEB=∠DFC,BF=CE,求证:△ABE≌△DCF.
如图,AB∥CD,∠AEB=∠DFC,BF=CE,求证:△ABE≌△DCF.