题目内容
20.(1)计算:($\frac{1}{2}$)-1+|-$\frac{\sqrt{12}}{3}$|-(2-$\sqrt{3}$)0+tan30°(2)解不等式组$\left\{\begin{array}{l}{\frac{x+3}{2}≥x}\\{3(x-1)>3}\end{array}\right.$.
分析 (1)首先计算负指数次幂、0次幂、化简二次根式、去掉绝对值符号,然后合并同类二次根式求解;
(2)首先解每个不等式,然后求得两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)原式=2+$\frac{2\sqrt{3}}{3}$-1+$\frac{\sqrt{3}}{3}$=1+$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{\frac{x+3}{2}≥x…①}\\{3(x-1)>3…②}\end{array}\right.$,
解①得x≤3,
解②得x>4.
则方程组无解.
点评 本题考查了一元一次不等式组的解法和实数的运算:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
10.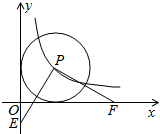 如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
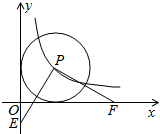 如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )
如图,点P在双曲线y=$\frac{4}{x}$上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是( )| A. | 6 | B. | 5 | C. | 4 | D. | 2$\sqrt{5}$ |
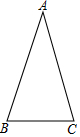 如图,在△ABC中,AB=AC,∠ABC=70°.
如图,在△ABC中,AB=AC,∠ABC=70°.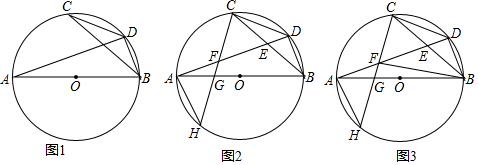
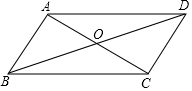 如图,在?ABCD中,∠CAB=90°,OA=1cm,OB=2cm,求AC,AD的长.
如图,在?ABCD中,∠CAB=90°,OA=1cm,OB=2cm,求AC,AD的长.