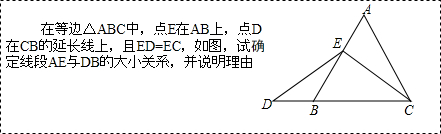
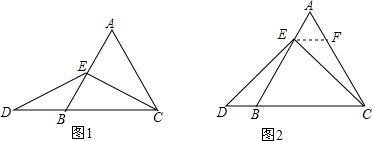
题目内容
12.已知在Rt△ABC中,∠C=90°,O为斜边AB上一点,以O为圆心,OA为半径作⊙O交斜边于另一点D,且AO=OD=DB.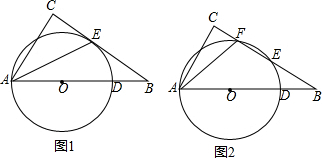
(1)如图1,⊙O与直角边BC相切于E点,连接AE,求cos∠CAE的值;
(2)如图2,⊙O与直角边BC相交于E、F两点,且E为$\widehat{DF}$的中点,连接AF,求cos∠CAF的值.
分析 (1)如图1,连接OE由BC与⊙O相切,得到OE⊥BC,由于AO=OD=DB,推出∠B=$\frac{1}{2}∠$BOE=30°,根据同圆的半径相等得到OA=OE,于是∠BAE=∠AEO=30°,进而求得结果cos∠CAE=$\frac{\sqrt{3}}{2}$;
(2)如图2,连接DF,OE,由垂径定理得到∴OE⊥DF,由AD是⊙O的直径,得到∠AFD=90°,根据平行线分线段成比例得到$\frac{OE}{AF}=\frac{OB}{AB}=\frac{BE}{BF}=\frac{2}{3}$,过O作OG⊥BC,同理可得$\frac{OG}{AC}=\frac{BO}{AB}=\frac{BG}{BC}=\frac{2}{3}$,于是得到结果
解答 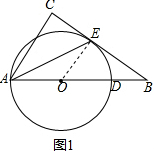 解:(1)如图1,连接OE,
解:(1)如图1,连接OE,
∵BC与⊙O相切,
∴OE⊥BC,
∵AO=OD=DB,
∴∠B=$\frac{1}{2}∠$BOE=30°,
∵OA=OE,
∴∠BAE=∠AEO=30°,
∴cos∠CAE=$\frac{\sqrt{3}}{2}$;
(2)如图2,连接DF,OE,
∵E为$\widehat{DF}$的中点,
∴OE⊥DF,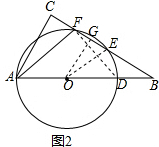
∵AD是⊙O的直径,
∴∠AFD=90°,
∴OE∥AF,
∴$\frac{OE}{AF}=\frac{OB}{AB}=\frac{BE}{BF}=\frac{2}{3}$,
过O作OG⊥BC,
∴OG∥AC,G为EF的中点,
∴$\frac{OG}{AC}=\frac{BO}{AB}=\frac{BG}{BC}=\frac{2}{3}$,
设圆的半径为 r,
∴r=$\sqrt{2}$EF,CF=$\frac{3}{4}$EF,
∴cos∠CAF=$\frac{\sqrt{14}}{4}$.
点评 本题考查了切线的性质,锐角三角函数,垂径定理,正确的作出辅助线是解题的关键.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案| A. | 7 | B. | 5 | C. | 3 | D. | 1 |
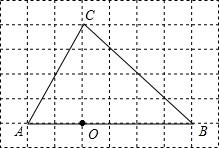 如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2.
如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2.
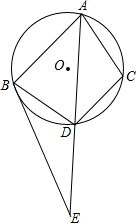 △ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.
△ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.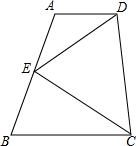 如图,在梯形ABCD中,AD∥BC,E是AB的中点.
如图,在梯形ABCD中,AD∥BC,E是AB的中点.