题目内容
6. 如图,在2×2正方形网格中,△ABC是以格点为顶点的三角形,则sin∠CAB=( )
如图,在2×2正方形网格中,△ABC是以格点为顶点的三角形,则sin∠CAB=( )| A. | $\frac{3}{2}\sqrt{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3}{10}$ |
分析 过C作CD⊥AB,利用勾股定理求出AB的长,三角形ABC面积等于正方形面积减去三个直角三角形面积,求出CD的长,利用锐角三角函数定义求出sin∠CAB的值即可.
解答 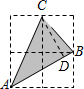 解:过C作CD⊥AB,
解:过C作CD⊥AB,
根据勾股定理得:ABCC=AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
S△ABC=4-1-$\frac{1}{2}$-1=1$\frac{1}{2}$=$\frac{1}{2}$CD•AB=$\frac{1}{2}$CD•$\sqrt{5}$,
解得:CD=$\frac{3\sqrt{5}}{5}$,
则sin∠CAB=$\frac{CD}{AC}$=$\frac{3}{5}$,
故选B.
点评 此题考查了勾股定理,以及锐角三角函数定义,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
18. 用一个平面去截一个圆柱体,截面不可能的是( )
用一个平面去截一个圆柱体,截面不可能的是( )
 用一个平面去截一个圆柱体,截面不可能的是( )
用一个平面去截一个圆柱体,截面不可能的是( )| A. |  | B. |  | C. |  | D. |  |
15.不等式x-5>-3的解集是( )
| A. | x>2 | B. | x>3 | C. | x>5 | D. | x<5 |
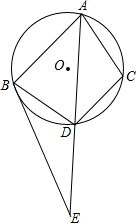 △ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.
△ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线. 如图,△ABC和△CDE都是等边三角形,P是线段AD的中点,Q是线段BE的中点.
如图,△ABC和△CDE都是等边三角形,P是线段AD的中点,Q是线段BE的中点.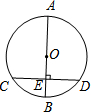 如图,AB是⊙O的直径,弦CD⊥AB于E,CE=3,则CD的长度是6.
如图,AB是⊙O的直径,弦CD⊥AB于E,CE=3,则CD的长度是6.