题目内容
5.在△ABC中,CA=CB,CD为AB边的中线,点P是线段AC上任意一点(不与点C重合),过点P作PE交CD于点E,使∠CPE=$\frac{1}{2}$∠CAB,过点C作CF⊥PE交PE的延长线于点F,交AB于点G.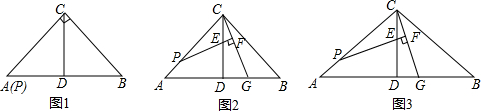
(1)如果∠ACB=90°,
①如图1,当点P与点A重合时,依题意补全图形,并指出与△CDG全等的一个三角形;
②如图2,当点P不与点A重合时,求$\frac{CF}{PE}$的值;
(2)如果∠CAB=a,如图3,请直接写出$\frac{CF}{PE}$的值.(用含a的式子表示)
分析 (1)①首先补全图形,如图1,易得AD=CD,∠EAD=22.5°,∠ECF=∠ACF-∠ACE=22.5°,即可得到△ADE(或△PDE)与△CDG全等;②过点P作PN∥AG交CG于点N,交CD于点M,如图2,易证△PFC≌△PFN,即可得到CF=FN=$\frac{1}{2}$CN,要求$\frac{CF}{PE}$的值,只需求出$\frac{CN}{PE}$,易证△PME≌△CMN,即可得到PE=CN,问题得以解决;
(2)过点P作PN∥AG交CG于点N,交CD于点M,如图3,同(1)②可得CF=$\frac{1}{2}$CN,易证△CMN∽△PME,则有$\frac{CN}{PE}$=$\frac{CM}{PM}$,然后在Rt△PMC中运用三角函数就可解决问题.
解答 解:(1)①作图,如图1所示.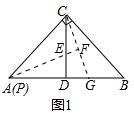
△ADE(或△PDE)与△CDG全等.
提示:只需证AD=CD,∠EAD=22.5°,∠ECF=22.5°即可;
②过点P作PN∥AG交CG于点N,交CD于点M,如图2,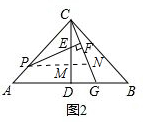
则有∠CPM=∠CAB.
∵∠CPE=$\frac{1}{2}$∠CAB,
∴∠CPE=$\frac{1}{2}$∠CPN,
∴∠CPE=∠FPN.
∵PF⊥CG,∴∠PFC=∠PFN=90°.
在△PFC和△PFN中,
$\left\{\begin{array}{l}{∠CPF=∠NPF}\\{PF=PF}\\{∠PFC=∠PFN}\end{array}\right.$,
∴△PFC≌△PFN,
∴CF=FN,PC=PN.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴∠A=∠B=45°,∠ADC=90°.
∵PN∥AB,
∴∠CPN=∠A=45°,∠PMC=∠ADC=90°.
∴∠PCN=∠PNC=67.5°,∠ACD=∠A=45°,
∴∠MCN=22.5°.
∵∠CPE=$\frac{1}{2}$∠CAB=22.5°,
∴∠EPM=22.5°,
∴∠EPM=∠MCN=22.5°.
∵∠CPM=∠PCM=45°,
∴PM=CM.
在△PME和△CMN中,
$\left\{\begin{array}{l}{∠EPM=∠MCN}\\{PM=CM}\\{∠EMP=∠NMC}\end{array}\right.$,
∴△PME≌△CMN,
∴PE=CN,
∴$\frac{CF}{PE}=\frac{CF}{CN}=\frac{1}{2}$;
(2)$\frac{CF}{PE}$=$\frac{1}{2}tanα$.
提示:过点P作PN∥AG交CG于点N,交CD于点M,如图3,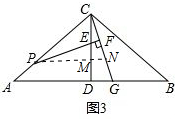
同(1)②可得CF=$\frac{1}{2}$CN.
易证△CMN∽△PME,
则有$\frac{CN}{PE}$=$\frac{CM}{PM}$.
∵tan∠CPN=$\frac{CM}{PM}$,∠CPM=∠A=α,
∴tanα=$\frac{CM}{PM}$=$\frac{CN}{PE}$=$\frac{2CF}{PE}$,
∴$\frac{CF}{PE}$=$\frac{1}{2}tanα$.
点评 本题主要考查了全等三角形的判定与性质、相似三角形的判定与性质、三角函数的定义、直角三角形的斜边上的中线等于斜边的一半、等腰三角形的性质等知识,通过添加辅助线把求$\frac{CF}{PE}$的值转化为求$\frac{CN}{PE}$的值是解决本题的关键.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案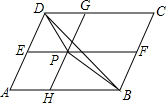 如图,点P为平行四边形ABCD内一点,过P点分别作AB、AD的平行线,交平行四边形ABCD的各边于点E、F、G、H.已知四边形AHPE的面积为3,四边形PFCG的面积为5,则△BDP的面积是1.
如图,点P为平行四边形ABCD内一点,过P点分别作AB、AD的平行线,交平行四边形ABCD的各边于点E、F、G、H.已知四边形AHPE的面积为3,四边形PFCG的面积为5,则△BDP的面积是1. | A. | x>2 | B. | x>3 | C. | x>5 | D. | x<5 |
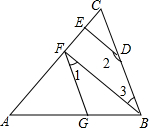 如图,∠AGF=∠ABC,∠1+∠2=180°.
如图,∠AGF=∠ABC,∠1+∠2=180°.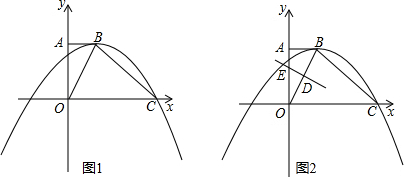
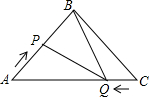 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.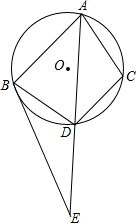 △ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.
△ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.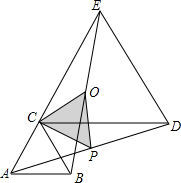 如图,△ABC和△CDE都是等边三角形,P是线段AD的中点,Q是线段BE的中点.
如图,△ABC和△CDE都是等边三角形,P是线段AD的中点,Q是线段BE的中点.