题目内容
2．已知反比例函数的图象经过点（a，b），则它的图象一定也经过（ ）| A． | （-a，-b） | B． | （a，-b） | C． | （-a，b） | D． | （a2，b2） |
分析 将（a，b）代入y=$\frac{k}{x}$即可求出k的值，再根据k=xy解答即可．
解答 解：因为反比例函数y=$\frac{k}{x}$的图象经过点（a，b），
故k=a×b=ab，
只有A选项中（-a）×（-b）=ab=k．
故选A．
点评 本题考查了反比例函数图象上点的坐标特征，只要点在函数的图象上，则一定满足函数的解析式．反之，只要满足函数解析式就一定在函数的图象上．
练习册系列答案
名校课堂系列答案
相关题目
10．下列运算错误的是（ ）
| A． | （-a）（-a）2=-a3 | B． | -2x2（-3x）=-6x4 | C． | （-a）3（-a）2=-a5 | D． | （-a）3（-a）3=a6 |
17．若a＜0，b＞0，则化简$\sqrt{{a}^{2}{b}^{3}}$的结果为（ ）
| A． | ab$\sqrt{ab}$ | B． | -ab$\sqrt{b}$ | C． | ab$\sqrt{b}$ | D． | ab2$\sqrt{b}$ |
7．某车间3月下旬生产零件的次品数如下（单位：个）：0，2，0，2，3，0，2，3，1，2，则在这10天中该车间生产的零件的次品数的（ ）
| A． | 众数是0 | B． | 极差是2 | C． | 平均数是2 | D． | 中位数是2 |
14．
如图，在平面直角坐标系中，⊙P的圆心坐标是（4，a）（a＞4），半径为4，函数y=x的图象被⊙P截得的弦AB的长为$2\sqrt{15}$，则⊙P的弦心距是1；a的值是4+$\sqrt{2}$．
如图，在平面直角坐标系中，⊙P的圆心坐标是（4，a）（a＞4），半径为4，函数y=x的图象被⊙P截得的弦AB的长为$2\sqrt{15}$，则⊙P的弦心距是1；a的值是4+$\sqrt{2}$． 
12．
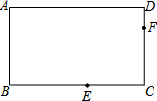在矩形ABCD中，点A关于角B的角平分线的对称点为E，点E关于角C的角平分线的对称点为F．若AD=$\sqrt{3}$AB=$\sqrt{3}$，则AF2=（ ）
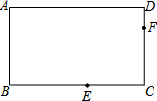在矩形ABCD中，点A关于角B的角平分线的对称点为E，点E关于角C的角平分线的对称点为F．若AD=$\sqrt{3}$AB=$\sqrt{3}$，则AF2=（ ）| A． | 8-4$\sqrt{3}$ | B． | 10-4$\sqrt{3}$ | C． | 8+4$\sqrt{3}$ | D． | 10+4$\sqrt{3}$ |