题目内容
13.解下列方程组:(1)$\left\{\begin{array}{l}{x-y=3}\\{3x-8y=14}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+4y=14}\\{\frac{x-3}{4}-\frac{y-3}{3}=\frac{1}{12}}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x-y=3①}\\{3x-8y=14②}\end{array}\right.$,
①×8-②得:5x=10,即x=2,
把x=2代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{x+4y=14①}\\{3x-4y=-2②}\end{array}\right.$,
①+②得:4x=12,即x=3,
把x=3代入①得:y=$\frac{11}{4}$,
则方程组解为$\left\{\begin{array}{l}{x=3}\\{y=\frac{11}{4}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
2.已知反比例函数的图象经过点(a,b),则它的图象一定也经过( )
| A. | (-a,-b) | B. | (a,-b) | C. | (-a,b) | D. | (a2,b2) |
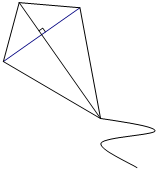 如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?
如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?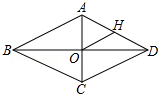 如图,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为28,求OH的长?
如图,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为28,求OH的长?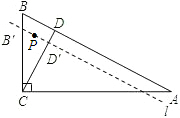 如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒. 根据图示,回答下列问题
根据图示,回答下列问题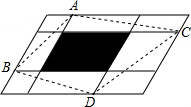 如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为100cm2,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形ABDC的面积是60cm2.
如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为100cm2,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形ABDC的面积是60cm2.