题目内容
14．是否存在x，使得当y=5时，分式$\frac{x+y}{{x}^{2}-{y}^{2}}$的值为0？若存在，求出x的值；若不存在，请说明理由．分析 分式的值为0，分子为0且分母不为0．
解答 解：不存在，理由如下：
把y=5代入$\frac{x+y}{{x}^{2}-{y}^{2}}$，得
$\frac{x+y}{{x}^{2}-{y}^{2}}$=$\frac{x+5}{{x}^{2}-{5}^{2}}$=$\frac{x+5}{（x+5）（x-5）}$．
当$\frac{x+y}{{x}^{2}-{y}^{2}}$=0，即$\frac{x+5}{（x+5）（x-5）}$=0时，
x+5=0且（x+5）（x-5）≠0，
则x无解．即这样的x的值不存在．
点评 本题考查了分式的值为零的条件．若分式的值为零，需同时具备两个条件：（1）分子为0；（2）分母不为0．这两个条件缺一不可．
练习册系列答案
相关题目
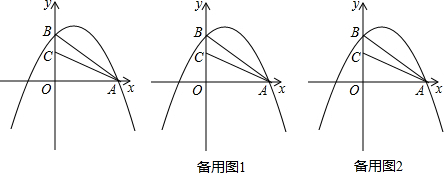
2．将图1的正四角锥ABCDE沿着其中的四个边剪开后，形成的展开图为图2．判断下列哪一个选项中的四个边可为此四个边？（ ）
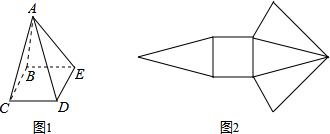
| A． | AC、AD、BC、DE | B． | AB、BE、DE、CD | C． | AC、BC、AE、DE | D． | AC、AD、AE、BC |
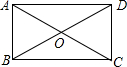如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=1，则BC的长为$\sqrt{3}$．
如图，面积为8cm2的正方形OABC的边OA，OC在坐标轴上，点P从点O出发，以每秒1个单位长度的速度沿x轴向点C运动；同时点Q从C点出发以相同的速度沿x轴的正方向运动，规定P点到达点C时，点Q也停止运动，过点Q作平行于y轴的直线l．连结AP，过P作AP的垂线交l于点D，连结AD，AD交BC于点E．设点P运动的时间为t秒．