题目内容
9.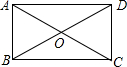 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.
分析 由矩形的性质得出∠ABC=90°,OA=OB,再证明△AOB是等边三角形,得出OA=AB,求出AC,然后根据勾股定理即可求出BC.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=1,
∴A=2OA=2,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 本题考查了矩形的性质、等边三角形的判定与性质以及勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
17.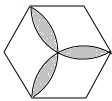 向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
 向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | $\frac{2\sqrt{3}-π}{π}$ | B. | $\frac{2π\sqrt{3}-9}{9}$ | C. | $\frac{π-\sqrt{3}}{π}$ | D. | $\frac{π\sqrt{3}-4}{9}$ |
1.下列三元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y+z=7}\\{2x+3y=5}\\{y+2x=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{xy=3}\\{y+z=2}\\{x+z=6}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{1}{x}+y+z=7}\\{2x+y+3z=5}\\{x+2y+z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=5}\\{3x+2y=9}\end{array}\right.$ |
19. 如图,点E在正方形ABCD的边AD上,已知AE=7,CE=13,则阴影部分的面积是( )
如图,点E在正方形ABCD的边AD上,已知AE=7,CE=13,则阴影部分的面积是( )
 如图,点E在正方形ABCD的边AD上,已知AE=7,CE=13,则阴影部分的面积是( )
如图,点E在正方形ABCD的边AD上,已知AE=7,CE=13,则阴影部分的面积是( )| A. | 114 | B. | 124 | C. | 134 | D. | 144 |
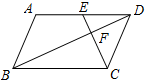 如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.
如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G. 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC. 如图,在四边形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点是边BC的三等分点,且AB=DC.求证:四边形AEFD是矩形.
如图,在四边形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点是边BC的三等分点,且AB=DC.求证:四边形AEFD是矩形.