题目内容
19.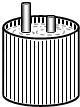 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,第一根露出水面的长度是它的$\frac{1}{3}$,第二根露出水面的长度是它的$\frac{1}{5}$.两根铁棒长度之和为55cm,求此时木桶中水的深度.若设此时木桶中水的深度为xcm,第一根铁棒的长为ycm,所列出的方程组为( )
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,第一根露出水面的长度是它的$\frac{1}{3}$,第二根露出水面的长度是它的$\frac{1}{5}$.两根铁棒长度之和为55cm,求此时木桶中水的深度.若设此时木桶中水的深度为xcm,第一根铁棒的长为ycm,所列出的方程组为( )| A. | $\left\{\begin{array}{l}{\frac{5}{4}x+y=55}\\{x=\frac{2}{3}y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=55}\\{\frac{2}{3}x=\frac{4}{5}y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\frac{3}{2}x+y=55}\\{y=\frac{4}{5}x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=55}\\{\frac{1}{3}y=\frac{1}{5}x}\end{array}\right.$ |
分析 设较长铁棒的长度为xcm,较短铁棒的长度为ycm.因为两根铁棒之和为55cm,故可的方程:x+y=55,又知两棒未露出水面的长度相等,又可得方程$\frac{2}{3}$x=$\frac{4}{5}$y,把两个方程联立,组成方程组.
解答 解:设较长铁棒的长度为xcm,较短铁棒的长度为ycm,
由题意得:$\left\{\begin{array}{l}{x+y=55}\\{\frac{2}{3}x=\frac{4}{5}y}\end{array}\right.$.
故选:B.
点评 此题主要考查了由实际问题抽象出二元一次方程组,关键是弄清题意,找出合适的等量关系,列出方程组.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.下列说法正确的是( )
| A. | 平方得16的数只有一个 | B. | 立方得-8的数只有一个 | ||
| C. | 平方得-9的数只有一个 | D. | 立方得9的整数只有一个 |
4.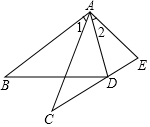 如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )
如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )
 如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )
如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )| A. | BD=CE | B. | AD=AE | C. | ∠B=∠C | D. | ∠ADB=∠AEC |
11.将(-30)0,(-3)2,($\frac{1}{5}$)-1这三个数按从小到大的顺序排列,正确的结果是( )
| A. | ($\frac{1}{5}$)-1<(-30)0<(-3)2 | B. | (-30)0<(-3)2<($\frac{1}{5}$)-1 | C. | (-3)2<($\frac{1}{5}$)-1<(-30)0 | D. | (-30)0<($\frac{1}{5}$)-1<(-3)2 |
 如图是一个由4个相同的长方体组成的立体图形,它的左视图是( )
如图是一个由4个相同的长方体组成的立体图形,它的左视图是( )



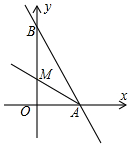 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴交于A,B两点,∠BAO的平分线所在的直线AM的解析式是y=-$\frac{1}{2}$x+3.
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴交于A,B两点,∠BAO的平分线所在的直线AM的解析式是y=-$\frac{1}{2}$x+3.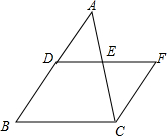 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.