题目内容
1.在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,5≤m<10时为B级,当0≤m<5为C级.现随机抽取30个符合年龄条件的青年人开展“每人日均发微博条数”的调查,所有抽青年人的“日均发微博条数”的数据如表:| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
| 13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
分析 (1)由抽取30个符合年龄条件的青年人中A级的有15人,即可求得样本数据中为A级的频率;
(2)根据题意得:1000个18~35岁的青年人中“日均发微博条数”为A级的人数为:1000×$\frac{1}{2}$=500;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与抽得2个人的“日均发微博条数”都是3的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵抽取30个符合年龄条件的青年人中A级的有15人,
∴样本数据中为A级的频率为:15÷30=0.5;
(2)1000个18~35岁的青年人中“日均发微博条数”为A级的人数为:1000×0.5=500(人);
(3)C级的有:0,2,3,3四人,
画树状图得: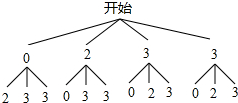
∵共有12种等可能的结果,抽得2个人的“日均发微博条数”都是3的有2种情况,
∴抽得2个人的“日均发微博条数”都是3的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是用列表法或画树状图法求概率、用频率估计概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
12.如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…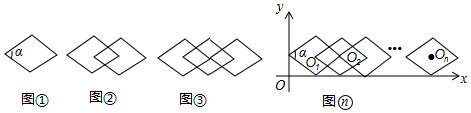
(1)观察图形并完成表格:
猜想:在图n中,菱形的个数为4n-5[用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1,1),则x1=$\sqrt{3}$;第2017个基本图形的中心O2017的坐标为(2017$\sqrt{3}$,1).

(1)观察图形并完成表格:
| 图形名称 | 基本图形的个数 | 菱形的个数 |
| 图① | 1 | 1 |
| 图② | 2 | 3 |
| 图③ | 3 | 7 |
| 图④ | 4 | 11 |
| … | … | … |
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1,1),则x1=$\sqrt{3}$;第2017个基本图形的中心O2017的坐标为(2017$\sqrt{3}$,1).
 如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠AOB等于130°.
如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠AOB等于130°.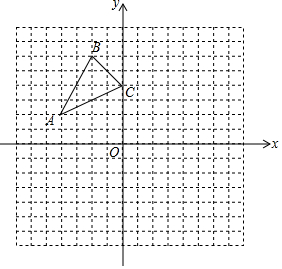 如图,已知A (-4,2),B (-2,6),C (0,4)是直角坐标系平面上三点.
如图,已知A (-4,2),B (-2,6),C (0,4)是直角坐标系平面上三点.
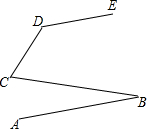 如图,AB∥DE,∠BCD=65°,∠CDE=135°,问∠ABC等于多少度?为什么?
如图,AB∥DE,∠BCD=65°,∠CDE=135°,问∠ABC等于多少度?为什么?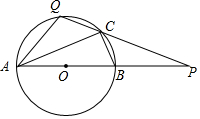 已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上)
已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上) 如图所示.在?ABCD中.E、F分别是边AD、BC上的点,连接AF、BE交于点G:连接CE、DF交于点H,连接GH.
如图所示.在?ABCD中.E、F分别是边AD、BC上的点,连接AF、BE交于点G:连接CE、DF交于点H,连接GH.