题目内容
6.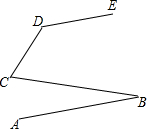 如图,AB∥DE,∠BCD=65°,∠CDE=135°,问∠ABC等于多少度?为什么?
如图,AB∥DE,∠BCD=65°,∠CDE=135°,问∠ABC等于多少度?为什么?
分析 过C作CF∥AB,根据平行线性质得出∠DCF+∠CDE=180°,∠B=∠BCF,求出∠DCF的度数,求出ABC度数即可.
解答 解:
过C作CF∥AB,
∵DE∥AB,
∴AB∥CF∥DE,
∴∠DCF+∠CDE=180°,∠B=∠BCF,
∵∠CDE=135°,
∴∠DCF=45°,
∵∠BCD=65°,
∴∠FCB=20°,
∴∠ABC=20°.
点评 本题考查了平行线的性质的应用,注意:①两直线平行,内错角相等,②两直线平行,同位角相等,③两直线平行,同旁内角互补.

练习册系列答案
相关题目
14.仪征市某活动中心组织一次少年跳绳比赛,各年龄组的参赛人数如表所示:
则全体参赛选手年龄的中位数是14岁.
| 年龄组 | 12岁 | 13岁 | 14岁 | 15岁 |
| 参赛人数 | 5 | 19 | 13 | 13 |
1.在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,5≤m<10时为B级,当0≤m<5为C级.现随机抽取30个符合年龄条件的青年人开展“每人日均发微博条数”的调查,所有抽青年人的“日均发微博条数”的数据如表:
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
| 13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
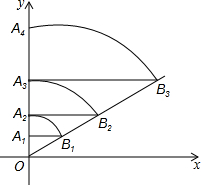 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2,再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,照此做法进行下去,点A2017的坐标为(0,22016).
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2,再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,照此做法进行下去,点A2017的坐标为(0,22016).