题目内容
10.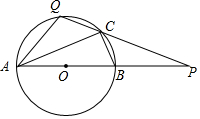 已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上)
已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上)
分析 根据圆内接四边形的性质即可得到∠QAP=∠BCP,故①正确;根据相似三角形的性质得到$\frac{PC}{PA}=\frac{PB}{PQ}$,故②错误;连接OQ,根据垂径定理得到OQ⊥AC,推出OQ∥BC,于是得到C是PQ的中点;故③正确;若点Q与C重合时,PQ=PC,于是得到PQ2=PA•PB,代入数据即可得到PQ=2$\sqrt{3}$,故④正确.
解答  解:∵四边形ABCQ是圆内接四边形,
解:∵四边形ABCQ是圆内接四边形,
∴∠QAP+∠BCQ=180°,
∵∠BCQ+∠BCP=180°,
∴∠QAP=∠BCP,故①正确;
∵∠P=∠P,
∴△PBC∽△PQA,
∴$\frac{PC}{PA}=\frac{PB}{PQ}$,故②错误;
连接OQ,
∵点Q为劣弧$\widehat{AC}$的中点,
∴$\widehat{AQ}$=$\widehat{CQ}$,
∴OQ⊥AC,
∵AB是⊙O的直径,
∴BC⊥AC,
∴OQ∥BC,
∵PB=OB,
∴PC=CQ,
∴C是PQ的中点;故③正确;
∵若点Q与C重合时,PQ=PC,
∵$\frac{PC}{PA}=\frac{PB}{PQ}$,
∴PQ2=PA•PB,
∵BP=OB=2,
∴PA=6,
∴PQ=2$\sqrt{3}$,故④正确,
故答案为:①③④.
点评 本题考查了相似三角形的判定和性质,圆周角定理,垂径定理,平行线的性质,掌握政策辅助线是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
1.在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,5≤m<10时为B级,当0≤m<5为C级.现随机抽取30个符合年龄条件的青年人开展“每人日均发微博条数”的调查,所有抽青年人的“日均发微博条数”的数据如表:
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
| 13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
7.函数y=$\frac{\sqrt{x+2}}{x-1}$的自变量取值范围是( )
| A. | -2≤x≤2 | B. | x≥-2且x≠1 | C. | x>-2 | D. | -2≤x≤2且x≠1 |
 如图,已知:∠1=∠4,∠1+∠2=180°,说明:AB∥CD,AB∥EF.
如图,已知:∠1=∠4,∠1+∠2=180°,说明:AB∥CD,AB∥EF.