题目内容
11. 如图所示.在?ABCD中.E、F分别是边AD、BC上的点,连接AF、BE交于点G:连接CE、DF交于点H,连接GH.
如图所示.在?ABCD中.E、F分别是边AD、BC上的点,连接AF、BE交于点G:连接CE、DF交于点H,连接GH.(1)当E、F分别是AD、BC的中点时,求证:四边形EGFH是平行四边形;
(2)试猜想,当AE与BF满足什么条件时.GH∥AD且GH=$\frac{1}{2}AD$.
分析 (1)可分别证明四边形AFCE是平行四边形,四边形BFDE是平行四边形,从而得出GF∥EH,GE∥FH,即可证明四边形EGFH是平行四边形;
(2)根据已知条件证得四边形ABFE是平行四边形,根据平行四边形的性质得到EG=BG,同理EH=CH,根据三角形的中位线定理得到②成立;不能证明四边形AFCE不是平行四边形,四边形不是BFDE是平行四边形,从而得出GF不平行EH,GE不平行FH,于是得到四边形EGFH不是平行四边形,①不成立.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵AE=$\frac{1}{2}$AD,FC=$\frac{1}{2}$BC,
∴AE∥FC,AE=FC.
∴四边形AECF是平行四边形.
∴GF∥EH.
同理可证:ED∥BF且ED=BF,
∴四边形BFDE是平行四边形.
∴GE∥FH.
∴四边形EGFH是平行四边形;
(2)当AE=BF时.GH∥AD且GH=$\frac{1}{2}AD$.
理由:连接EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.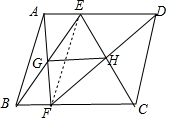
∵AE=BF,
∴DE=CF,
∵AE∥BF,DE∥CF,
∴四边形ABFE是平行四边形,讨论四边形EFCD是平行四边形,
∴AG=FG,FH=DH,
GH=$\frac{1}{2}$AD,GH∥AD.
点评 本题考查了平行四边形的判定和性质,三角形的中位线定理等知识,解题的关键是熟练掌握平行四边形的判定和性质,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,5≤m<10时为B级,当0≤m<5为C级.现随机抽取30个符合年龄条件的青年人开展“每人日均发微博条数”的调查,所有抽青年人的“日均发微博条数”的数据如表:
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
| 13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
7.函数y=$\frac{\sqrt{x+2}}{x-1}$的自变量取值范围是( )
| A. | -2≤x≤2 | B. | x≥-2且x≠1 | C. | x>-2 | D. | -2≤x≤2且x≠1 |