题目内容
16. 如图,四边形ABCD是平行四边形,DE⊥AB于点E,BF⊥DC于点F,请用尽可能多的方法证明:△ADE≌△CBF.
如图,四边形ABCD是平行四边形,DE⊥AB于点E,BF⊥DC于点F,请用尽可能多的方法证明:△ADE≌△CBF.
分析 由平行四边形的性质得出∠A=∠C,AD=CB,AB∥CD,AB=CD,由AAS、HL、SAS证明△ADE≌△CBF即可.
解答 证明:方法1:
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB,AB∥CD,AB=CD,
∵DE⊥AB于点E,BF⊥DC于点F,
∴∠AED=∠CFB,
在△ADE和△CBF中,$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{∠AED=∠CFB}&{\;}\\{AD=CB}&{\;}\end{array}\right.$,
∴△ADE≌△CBF(AAS).
方法2:
∵DE⊥AB于点E,BF⊥DC于点F,
∴DE∥FB,
又∵DF∥BE,
∴四边形BFDE是平行四边形,
∴DE=BF,DF=BE,
在Rt△ADE和Rt△CBF中,$\left\{\begin{array}{l}{AD=CB}\\{DE=BF}\end{array}\right.$,
∴Rt△ADE≌Rt△CBF(HL);
方法3:
∵AB=CD,BE=DF,
∴AE=CF,
在△ADE和△CBF中,$\left\{\begin{array}{l}{AD=CB}&{\;}\\{∠A=∠C}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△ADE≌△CBF.
点评 本题考查了平行四边形的性质、全等三角形的判定方法;熟练掌握平行四边形的性质,灵活运用三角形全等的判定方法是解决问题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
6.下列说法中,正确的是( )
| A. | 4的算术平方根是2 | B. | 16的平方根是4 | ||
| C. | 9的算术平方根是±3 | D. | -a没有平方根 |
7.下列方程中是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{x}$=0 | B. | x2+3x=x2-1 | C. | (x-1)(x-2)=2 | D. | 3x2-2y=0 |
1.某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)若商场要获利28050元,则销售单价应走为多少元?
(3)如果你是该商场经理,你将如何决策使商场能获得最大盈利?
| 销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
| 销售量y(件) | … | 440 | 430 | 420 | 410 | … |
(2)若商场要获利28050元,则销售单价应走为多少元?
(3)如果你是该商场经理,你将如何决策使商场能获得最大盈利?
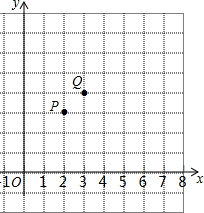 如图,坐标系中有两点P(2,3),Q(3,4).
如图,坐标系中有两点P(2,3),Q(3,4). 一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.
一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.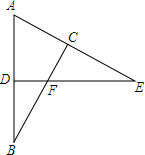 在△ADE中,∠E=22°,延长AD至点B,使得BD=AD,过B点作BC⊥AE,垂足点C,线段BC交边DE于点F,且EF=AB,求∠ADE.
在△ADE中,∠E=22°,延长AD至点B,使得BD=AD,过B点作BC⊥AE,垂足点C,线段BC交边DE于点F,且EF=AB,求∠ADE.