题目内容
6.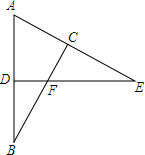 在△ADE中,∠E=22°,延长AD至点B,使得BD=AD,过B点作BC⊥AE,垂足点C,线段BC交边DE于点F,且EF=AB,求∠ADE.
在△ADE中,∠E=22°,延长AD至点B,使得BD=AD,过B点作BC⊥AE,垂足点C,线段BC交边DE于点F,且EF=AB,求∠ADE.
分析 取EF中点G,连结CD、CG.根据直角三角形斜边上的中线等于斜边的一半得出CD=AD=BD=$\frac{1}{2}$AB,CG=EG=FG=$\frac{1}{2}$EF,由EF=AB,得到CG=CD,那么∠CDG=∠CGD.再根据等边对等角的性质以及三角形外角的性质求出∠GCE=∠E=22°,∠CGD=∠GCE+∠E=44°,∠CDG=∠CGD=44°,∠ACD=∠CDG+∠E=44°+22°=66°,∠A=∠ACD=66°,然后根据三角形内角和定理得到∠ADE=180°-∠A-∠E=92°.′
解答 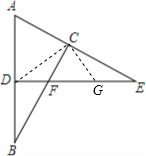 解:如图,取EF中点G,连结CD、CG.
解:如图,取EF中点G,连结CD、CG.
∵BC⊥AE,垂足点C,
∴∠ACB=∠ECF=90°,
∵BD=AD,EF中点G,
∴CD=AD=BD=$\frac{1}{2}$AB,CG=EG=FG=$\frac{1}{2}$EF,
∵EF=AB,
∴CG=CD,
∴∠CDG=∠CGD.
∵CG=EG,
∴∠GCE=∠E=22°,
∴∠CGD=∠GCE+∠E=44°,
∴∠CDG=∠CGD=44°,
∴∠ACD=∠CDG+∠E=44°+22°=66°.
在△ACD中,∵CD=AD,
∴∠A=∠ACD=66°,
∴∠ADE=180°-∠A-∠E=180°-66°-22°=92°.
点评 本题考查了直角三角形的性质,等腰三角形的判定与性质,三角形外角的性质,三角形内角和定理,难度适中.根据直角三角形斜边上的中线等于斜边的一半作出辅助线构造等腰三角形CDG是解题的关键.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
1.某自行车厂计划一周生产自行车2100辆,平均每天生产300辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正,减产记为负):
(1)根据上表记录的数据,可知该厂星期五生产自行车290辆;
(2)根据上表记录的数据,可知该厂本周实际共生产自行车2108辆;
(3)产量最多的一天比产量最少的一天多生产自行车26辆;
(4)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖25元;少生产一辆扣30元,那么该厂工人这一周的工资总额是多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +12 | -10 | +16 | -9 |
(2)根据上表记录的数据,可知该厂本周实际共生产自行车2108辆;
(3)产量最多的一天比产量最少的一天多生产自行车26辆;
(4)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖25元;少生产一辆扣30元,那么该厂工人这一周的工资总额是多少元?
 如图,四边形ABCD是平行四边形,DE⊥AB于点E,BF⊥DC于点F,请用尽可能多的方法证明:△ADE≌△CBF.
如图,四边形ABCD是平行四边形,DE⊥AB于点E,BF⊥DC于点F,请用尽可能多的方法证明:△ADE≌△CBF. 如图,△ABC的三个顶点的坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.
如图,△ABC的三个顶点的坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.