题目内容
10.解不等式组:$\left\{\begin{array}{l}{x+3≥2x-1①}\\{3x-5≥1②}\end{array}\right.$,请结合题意填空,完成本题的解答:(1)解不等式①,得:x≤4;
(2)解不等式②,得:x≥2;
(3)把不等式①和②的解集在数轴上表示出来:
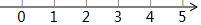
(4)原不等式的解集为:2≤x≤4.
分析 (1)移项、合并同类项即可求解;
(2)去括号、移项、合并同类项、系数化成1即可求解;
(3)把(1)和(2)求得解集在数轴上表示出来即可;
(4)两个解集的公共部分就是不等式组的解集.
解答 解:(1)移项,得x-2x≥-1-3,
合并同类项,得-x≥-4,
系数化成1得x≤4.
故答案是:x≤4;
(2)移项,得3x≥1+5,
合并同类项,得3x≥6,
系数化成1得x≥2.
故答案是:x≥2;
(3) ;
;
(4)不等式组的解集是2≤x≤4.
故答案是:2≤x≤4.
点评 本题考查了解一元一次不等式组:求不等式组的解集的过程叫解不等式组.解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
18.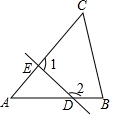 如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为( )
如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为( )
 如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为( )
如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为( )| A. | 130° | B. | 180° | C. | 230° | D. | 260° |
15. 己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
 己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | 1<|a|<b | B. | 1<-a<b | C. | |a|<1<|b| | D. | -b<a<-1 |
20.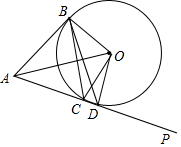 从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )
从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )
 从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )
从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )| A. | ∠COD=30° | B. | AB⊥OB | C. | AB∥OC | D. | ∠ABC=60° |
 如图,已知A(1,6)B(n,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线与y轴交于C点.
如图,已知A(1,6)B(n,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线与y轴交于C点.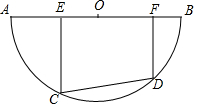 如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.
如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.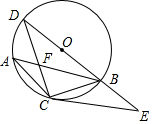 如图,AB是⊙O的弦,C是劣弧$\widehat{AB}$的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
如图,AB是⊙O的弦,C是劣弧$\widehat{AB}$的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.


