题目内容
2.下列说法正确的是( )| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形四边中点顺次连接成的四边形是矩形 | |
| C. | 三个角的度数之比为1:$\sqrt{3}$:2的三角形是直角三角形 | |
| D. | 对角线互相垂直的平行四边形是正方形 |
分析 根据平行四边形的判定、直角三角形的判定和正方形的判定定理判断即可.
解答 解:一组对边平行,另一组对边相等的四边形不一定是平行四边形,A错误;
对角线互相垂直的四边形四边中点顺次连接成的四边形是矩形,B正确;
三边之比为1:$\sqrt{3}$:2的三角形是直角三角形,但三个角的度数之比为1:$\sqrt{3}$:2的三角形不一定是直角三角形,C错误;
对角线互相垂直且相等的平行四边形是正方形,D错误,
故选:B.
点评 本题考查的是命题的真假判断,掌握平行四边形的判定、直角三角形的判定和正方形的判定定理是解题的关键.

练习册系列答案
相关题目
13.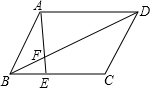 如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
 如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )| A. | 4:5 | B. | 4:9 | C. | 5:9 | D. | 4:10 |
10. 一只自由飞行的小鸟,将随意地落在如图的方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为( )
一只自由飞行的小鸟,将随意地落在如图的方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为( )
 一只自由飞行的小鸟,将随意地落在如图的方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为( )
一只自由飞行的小鸟,将随意地落在如图的方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为( )| A. | $\frac{64}{225}$ | B. | $\frac{7}{15}$ | C. | $\frac{49}{225}$ | D. | $\frac{8}{15}$ |
7.已知关于x的方程2x+m=3的解是x=1,则m的值为( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
11.下列说法正确的是( )
| A. | 延长射线得直线 | B. | 过两点有且只有一条直线 | ||
| C. | 直线就是一个平角 | D. | 过三点一定能作三条直线 |
12. 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠D=∠DCE | D. | ∠D+∠ACD=180° |
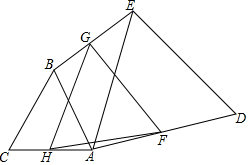 如图,两个等边△ABC、△ADE(顶点依逆时针方向排列),F、G、H分别是AD、BE、AC的中点,求证:△FGH是等边三角形.
如图,两个等边△ABC、△ADE(顶点依逆时针方向排列),F、G、H分别是AD、BE、AC的中点,求证:△FGH是等边三角形.