题目内容
10. 一只自由飞行的小鸟,将随意地落在如图的方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为( )
一只自由飞行的小鸟,将随意地落在如图的方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为( )| A. | $\frac{64}{225}$ | B. | $\frac{7}{15}$ | C. | $\frac{49}{225}$ | D. | $\frac{8}{15}$ |
分析 根据几何概率的求法:小鸟落在阴影方格地面上的概率即该区域的面积与总面积的比值.
解答 解:因为所有方格面积为:S1=15;
阴影的面积为:S2=7.
所以小鸟落在阴影方格地面上的概率是$\frac{7}{15}$.
故选:B.
点评 本题考查了几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
相关题目
1.下列各组中的两个项不属于同类项的是( )
| A. | 3x2y和-2x2y | B. | a2和32 | C. | -1和$1\frac{1}{4}$ | D. | -xy和2yx |
18. 如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
 如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )| A. | 两点确定一条直线 | B. | 垂线段最短 | ||
| C. | 两点之间,线段最短 | D. | 两点之间,直线最短 |
15.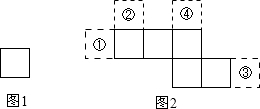 图1和图2中所有的正方形都全等,将图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )
图1和图2中所有的正方形都全等,将图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )
 图1和图2中所有的正方形都全等,将图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )
图1和图2中所有的正方形都全等,将图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
2.下列说法正确的是( )
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形四边中点顺次连接成的四边形是矩形 | |
| C. | 三个角的度数之比为1:$\sqrt{3}$:2的三角形是直角三角形 | |
| D. | 对角线互相垂直的平行四边形是正方形 |
19.下列计算正确的是( )
| A. | $\sqrt{2}+\sqrt{5}=\sqrt{7}$ | B. | $3\sqrt{2}-\sqrt{2}=3$ | C. | (3a)2=9a | D. | $\frac{3}{{\sqrt{3}}}=\sqrt{3}$ |
20.在平面直角坐标系中,抛物线y=x2-1与坐标轴交点的个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |