题目内容
13.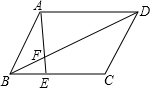 如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )| A. | 4:5 | B. | 4:9 | C. | 5:9 | D. | 4:10 |
分析 由平行四边形的性质可证△BEF∽△DAF,再利用相似三角形的性质可求得BE:AD=BF:FD,结合条件可求得答案.
解答 解:
∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∵BE:EC=4:1,
∴BE:AD=BE:BC=4:5,
∵AD∥BC,
∴∠BEF=∠DAF,∠EBF=∠ADF,
∴△BEF∽△DAF,
∴BF:FD=BE:AD=4:5,
故选A.
点评 本题主要考查相似三角形的判定和性质,利用相似三角形的性质把所求问题转化为求BE:AD是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
1.下列各组中的两个项不属于同类项的是( )
| A. | 3x2y和-2x2y | B. | a2和32 | C. | -1和$1\frac{1}{4}$ | D. | -xy和2yx |
8.在实数-$\frac{22}{7}$、0、-$\sqrt{3}$、506、π、0.0101中,无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18. 如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
 如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )| A. | 两点确定一条直线 | B. | 垂线段最短 | ||
| C. | 两点之间,线段最短 | D. | 两点之间,直线最短 |
2.下列说法正确的是( )
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形四边中点顺次连接成的四边形是矩形 | |
| C. | 三个角的度数之比为1:$\sqrt{3}$:2的三角形是直角三角形 | |
| D. | 对角线互相垂直的平行四边形是正方形 |
3.已知函数y=(m-2)x${\;}^{{m}^{2}-2}$+4x+7是二次函数,则m的值为( )
| A. | -2 | B. | ±2 | C. | $\sqrt{3}$ | D. | ±$\sqrt{3}$ |
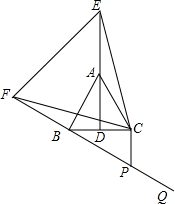 如图,在等边△ABC中,已知AD是∠BAC的角平分线,E为AD延长线上一点,以CE为一边且在CE以左作等边△CEF,连接BF.
如图,在等边△ABC中,已知AD是∠BAC的角平分线,E为AD延长线上一点,以CE为一边且在CE以左作等边△CEF,连接BF. 如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.
如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.