题目内容
 如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:欲证明∠1=∠2,只需证得四边形EDFB是平行四边形或△ABF≌△CDE即可.
解答: 解:方法一:
解:方法一:
补充条件①BE∥DF.
证明:如图,∵BE∥DF,
∴∠BEC=∠DFA,
∴∠BEA=∠DFC,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∴四边形BFDE是平行四边形,
∴ED∥BF,
∴∠1=∠2;
方法二:
补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS),
∴∠1=∠2.
 解:方法一:
解:方法一:补充条件①BE∥DF.
证明:如图,∵BE∥DF,
∴∠BEC=∠DFA,
∴∠BEA=∠DFC,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE与△CDF中,
|
∴△ABE≌△CDF(ASA),
∴BE=DF,
∴四边形BFDE是平行四边形,
∴ED∥BF,
∴∠1=∠2;
方法二:
补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△ABF与△CDE中,
|
∴△ABF≌△CDE(SAS),
∴∠1=∠2.
点评:本题考查了平行四边形的判定与性质,全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知:
=0.325,
=32.5,则
=( )
| a |
| b |
| a |
| b |
| A、10-1 |
| B、10-2 |
| C、10-3 |
| D、10-4 |
 如图,在正方形ABCD中,点G是BC上任意一点,连接AG,过点B,D分别作BF⊥AG,DE⊥AG,垂足分别为点F,E.
如图,在正方形ABCD中,点G是BC上任意一点,连接AG,过点B,D分别作BF⊥AG,DE⊥AG,垂足分别为点F,E.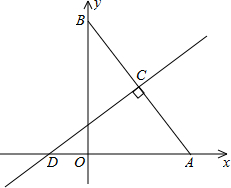 如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB),且OA、OB的长分别是一元二次方程x2-14x+48=0的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D,点P是直线CD上一个动点,点Q是直线AB上一个动点.
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB),且OA、OB的长分别是一元二次方程x2-14x+48=0的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D,点P是直线CD上一个动点,点Q是直线AB上一个动点.